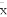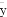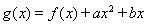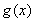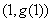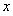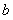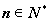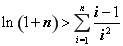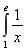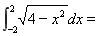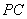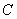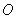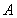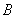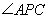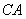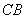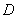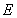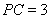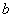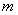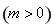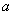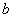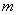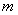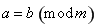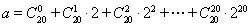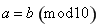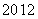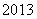题目内容
已知双曲线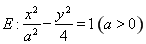 的中心为原点
的中心为原点 ,左、右焦点分别为
,左、右焦点分别为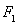 、
、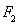 ,离心率为
,离心率为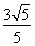 ,点
,点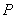 是直线
是直线 上任意一点,点
上任意一点,点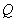 在双曲线
在双曲线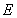 上,且满足
上,且满足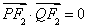 .
.
(1)求实数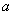 的值;
的值;
(2)证明:直线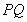 与直线
与直线 的斜率之积是定值;
的斜率之积是定值;
(3)若点 的纵坐标为
的纵坐标为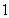 ,过点
,过点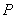 作动直线
作动直线 与双曲线右支交于不同的两点
与双曲线右支交于不同的两点 、
、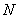 ,在线段
,在线段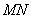 上去异于点
上去异于点 、
、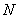 的点
的点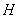 ,满足
,满足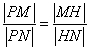 ,证明点
,证明点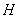 恒在一条定直线上.
恒在一条定直线上.
(1)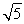 ;(2)详见解析;(3)详见解析.
;(2)详见解析;(3)详见解析.
【解析】
试题分析:(1)根据双曲线的离心率列方程求出实数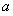 的值;(2)设点
的值;(2)设点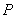 的坐标为
的坐标为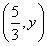 ,点
,点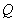 的坐标为
的坐标为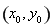 ,利用条件
,利用条件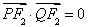 确定
确定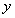 与
与 、
、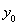 之间的关系,再结合点
之间的关系,再结合点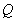 在双曲线
在双曲线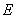 上这一条件,以及斜率公式来证明直线
上这一条件,以及斜率公式来证明直线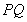 与直线
与直线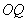 的斜率之积是定值;(3)证法一是先设点
的斜率之积是定值;(3)证法一是先设点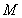 、
、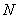 的坐标分别为
的坐标分别为 、
、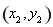 ,结合(2)得到
,结合(2)得到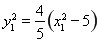 ,
,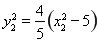 ,引入参数
,引入参数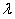 ,利用
,利用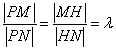 转化为相应的条件
转化为相应的条件 ,利用坐标运算得到点
,利用坐标运算得到点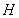 的坐标所满足的关系式
的坐标所满足的关系式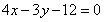 ,进而证明点
,进而证明点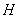 恒在定直线
恒在定直线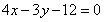 上;证法二是设直线
上;证法二是设直线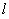 的方程为
的方程为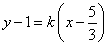 ,将直线
,将直线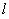 的方程与双曲线的方程联立,结合韦达定理,将条件
的方程与双曲线的方程联立,结合韦达定理,将条件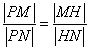 进行等价转化为
进行等价转化为 ,结合韦达定理化简为
,结合韦达定理化简为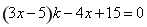 ,最后利用点
,最后利用点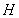 在直线
在直线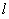 上得到
上得到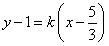 ,从而消去
,从而消去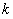 得到
得到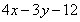
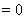 ,进而证明点
,进而证明点 恒在定直线
恒在定直线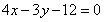 上.
上.
试题解析:(1)根据双曲线的定义可得双曲线的离心率为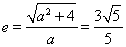 ,由于
,由于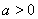 ,解得
,解得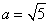 ,
,
故双曲线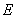 的方程为
的方程为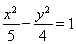 ;
;
(2)设点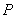 的坐标为
的坐标为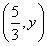 ,点
,点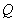 的坐标为
的坐标为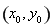 ,易知点
,易知点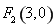 ,
,
则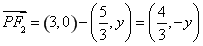 ,
,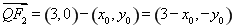 ,
,
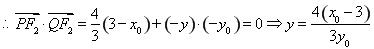 ,因此点
,因此点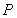 的坐标为
的坐标为 ,
,
故直线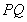 的斜率
的斜率 ,直线
,直线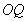 的斜率为
的斜率为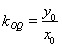 ,
,
因此直线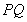 与直线
与直线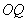 的斜率之积为
的斜率之积为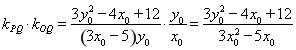 ,
,
由于点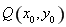 在双曲线
在双曲线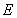 上,所以
上,所以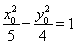 ,所以
,所以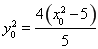 ,
,
于是有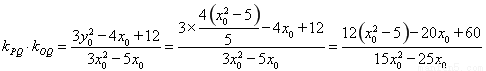
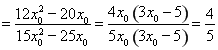 (定值);
(定值);
(3)证法一:设点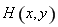 且过点
且过点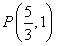 的直线
的直线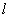 与双曲线
与双曲线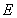 的右支交于不同的两点
的右支交于不同的两点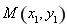 、
、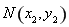 ,由(2)知,
,由(2)知,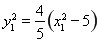 ,
,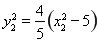 ,
,
设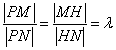 ,则
,则 ,即
,即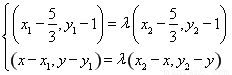 ,
,
整理得 ,
,
由①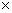 ③,②
③,②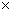 ④得,
④得, ,
,
将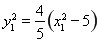 ,
,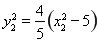 ,代入⑥得
,代入⑥得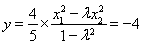 ,⑦,
,⑦,
将⑦代入⑤得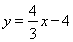 ,即点
,即点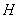 恒在定直线
恒在定直线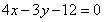 上;
上;
证法二:依题意,直线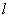 的斜率
的斜率 存在,设直线
存在,设直线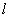 的方程为
的方程为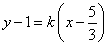 ,
,
由 ,
,
消去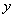 得
得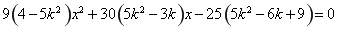 ,
,
因为直线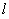 与双曲线
与双曲线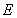 的右支交于不同的两点
的右支交于不同的两点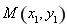 、
、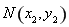 ,
,
则有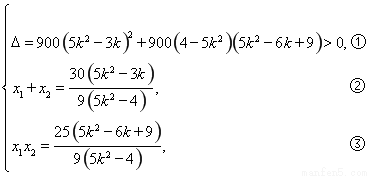 ,
,
设点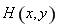 ,由
,由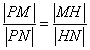 ,得
,得 ,
,
整理得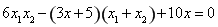 ,
,
将②③代入上式得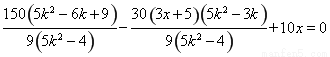 ,
,
整理得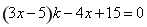 ,④
,④
因为点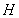 在直线
在直线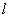 上,所以
上,所以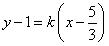 ,⑤
,⑤
联立④⑤消去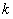 得
得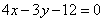 ,所以点
,所以点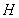 恒在定直线
恒在定直线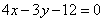 .
.
考点:1.双曲线的离心率;2.向量的坐标运算;3.斜率公式;4.韦达定理

 优加精卷系列答案
优加精卷系列答案