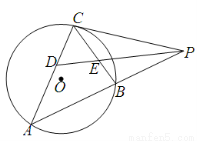
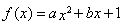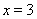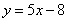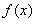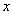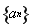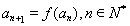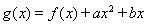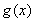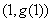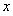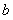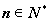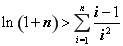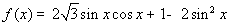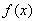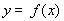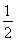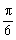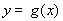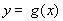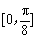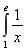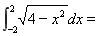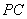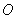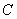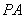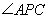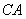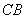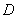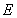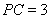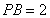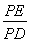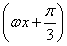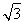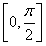题目内容
设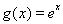 ,
,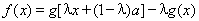 ,其中
,其中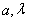 是常数,且
是常数,且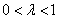 .
.
(1)求函数 的极值;
的极值;
(2)证明:对任意正数 ,存在正数
,存在正数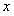 ,使不等式
,使不等式 成立;
成立;
(3)设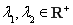 ,且
,且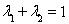 ,证明:对任意正数
,证明:对任意正数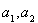 都有:
都有: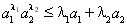 .
.
(1)当 时,
时, 取极大值,但
取极大值,但 没有极小值(2)见解析(3)见解析
没有极小值(2)见解析(3)见解析
【解析】(1)∵ , -----------------1分
, -----------------1分
由 得,
得,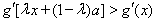 ,
,
∴ ,即
,即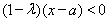 ,解得
,解得 ,-----------------3分
,-----------------3分
故当 时,
时, ;当
;当 时,
时, ;
;
∴当 时,
时, 取极大值,但
取极大值,但 没有极小值.-----------------4分
没有极小值.-----------------4分
(2)∵ ,
,
又当 时,令
时,令 ,则
,则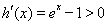 ,
,
故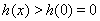 ,
,
因此原不等式化为 ,即
,即 , -----------------6分
, -----------------6分
令 ,则
,则 ,
,
由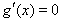 得:
得: ,解得
,解得 ,
,
当 时,
时, ;当
;当 时,
时, .
.
故当 时,
时, 取最小值
取最小值 ,-----------------8分
,-----------------8分
令 ,则
,则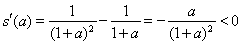 .
.
故 ,即
,即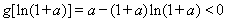 .
.
因此,存在正数 ,使原不等式成立.-----------------10分
,使原不等式成立.-----------------10分
(3)对任意正数 ,存在实数
,存在实数 使
使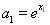 ,
,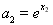 ,
,
则 ,
, ,
,
原不等式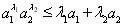
 ,
,
 -----------------14分
-----------------14分
由(1) 恒成立,
恒成立,
故 ,
,
取 ,
,
即得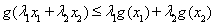 ,
,
即 ,故所证不等式成立. -----------------14分
,故所证不等式成立. -----------------14分

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目