题目内容
【题目】函数f（x）= 
，若f（0）是f（x）的最小值，则a的取值范围为（ ）
A.[﹣1，2]
B.[﹣1，0]
C.[1，2]
D.[0，2]
【答案】D
【解析】解：由于f（x）=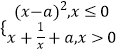 
， 则当x=0时，f（0）=a2 ，
由于f（0）是f（x）的最小值，
则（﹣∞，0]为减区间，即有a≥0，
则有a2≤x+ 
+a，x＞0恒成立，
由x+ ≥2 
=2，当且仅当x=1取最小值2，
则a2≤2+a，解得﹣1≤a≤2．
综上，a的取值范围为[0，2]．
故选：D．
【考点精析】解答此题的关键在于理解函数的最值及其几何意义的相关知识，掌握利用二次函数的性质（配方法）求函数的最大（小）值；利用图象求函数的最大（小）值；利用函数单调性的判断函数的最大（小）值．
练习册系列答案
相关题目
【题目】为了促进学生的全面发展，郑州市某中学重视学生社团文化建设，现用分层抽样的方法从“话剧社”，“创客社”，“演讲社”三个金牌社团中抽取6人组成社团管理小组，有关数据见表（单位：人）：
社团名称 | 成员人数 | 抽取人数 |
话剧社 | 50 | a |
创客社 | 150 | b |
演讲社 | 100 | c |
（1）求a，b，c的值；
（2）若从“话剧社”，“创客社”，“演讲社”已抽取的6人中任意抽取2人担任管理小组组长，求这2人来自不同社团的概率．
