题目内容
【题目】如图所示，两圆内切于点T，大圆的弦AB切小圆于点C.TA，TB与小圆分别相交于点E，F.FE的延长线交两圆的公切线TP于点P.
求证：(1) 
＝
；
(2)AC·PF＝BC·PT.
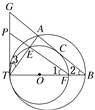
【答案】(1) 见解析(2) 见解析
【解析】试题分析：（1）根据内错角相等得EF∥AB，再由相切得OC⊥EF，即得结论（2）由切割线定理得AC·TE＝BC·TF.再根据三角形相似得PT·TF＝PF·TE,即得结论
试题解析：证明：(1)设小圆的圆心为点O，连接OC.
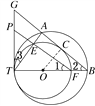∵AB切小圆于点C，∴OC⊥AB.
∵∠1＝∠3＝∠2，
∴EF∥AB，∴OC⊥EF，
∴
.
(2)∵EF∥AB，∴
＝
＝
.
∵AB切小圆于点C，
∴AC2＝AE·AT，BC2＝BF·BT.
∴
＝
＝
，
＝.
∵PT是公切线，∴∠PTF＝90°，
∵TF是⊙O的直径，
∴TE⊥PF，△PTF∽△TEF，
∴
＝，∴＝，
∴AC·PF＝BC·PT.
练习册系列答案
相关题目
