题目内容
15．某几何体三视图如图（单位；cm），则该几何体的体积是（ ）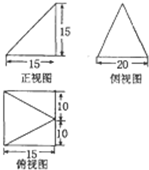
| A． | 1500cm3 | B． | 1025cm3 | C． | 625cm3 | D． | 1200cm3 |
分析 根据几何体的三视图，得出该几何体是底面为矩形的直四棱锥，结合图中数据求出它的体积．
解答 
解：根据几何体的三视图，得；
该几何体是底面为矩形，高为15cm的直四棱锥；
且底面矩形的长为20cm，宽为15cm，
如图所示；
∴该四棱锥的体积为$\frac{1}{3}$×20×15×15=1500cm2．
故选：A．
点评 本题考查了空间几何体的三视图的应用问题，也考查了空间想象能力与数据的计算能力，是基础题目．
练习册系列答案
相关题目
5．sin600°=（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{\sqrt{3}}{2}$ | C． | -$\frac{1}{2}$ | D． | -$\frac{\sqrt{3}}{2}$ |
3．若0＜a＜1，0＜b＜1且a≠b，则a+b、2$\sqrt{ab}$、2ab、a2+b2中最大的一个是（ ）
| A． | a+b | B． | 2$\sqrt{ab}$ | C． | 2ab | D． | a2+b2 |
7．
如图是一个空间几何体的三视图，该几何体的外接球的体积为（ ）
如图是一个空间几何体的三视图，该几何体的外接球的体积为（ ）| A． | 8$\sqrt{2}$ | B． | $\frac{8\sqrt{2}π}{3}$ | C． | 4$\sqrt{2}$π | D． | $\frac{16\sqrt{2}π}{3}$ |
5．在△ABC中，AB=3，BC=$\sqrt{13}$，AC=4，则AC边上的高等于（ ）
| A． | $\frac{3}{2}$$\sqrt{3}$ | B． | $\frac{3}{2}$$\sqrt{2}$ | C． | 3 | D． | 3$\sqrt{3}$ |