题目内容
6.已知设Sn为等比数列{an}的前n项和,S4=5S2,求$\frac{{a}_{2}•{a}_{7}}{{a}_{{4}^{2}}}$的值.分析 设等比数列{an}的公比为q,由于S4=5S2,可得${a}_{1}(1+q+{q}^{2}+{q}^{3})$=5a1(1+q),解得q.再利用等比数列的通项公式可得$\frac{{a}_{2}•{a}_{7}}{{a}_{{4}^{2}}}$=q.
解答 解:设等比数列{an}的公比为q,
∵S4=5S2,
∴${a}_{1}(1+q+{q}^{2}+{q}^{3})$=5a1(1+q),
化为(1+q)(q-2)(q+2)=0,
解得q=-1,±2.
∴$\frac{{a}_{2}•{a}_{7}}{{a}_{{4}^{2}}}$=$\frac{{a}_{1}q•{a}_{1}{q}^{6}}{({a}_{1}{q}^{3})^{2}}$=q=-1或±2.
点评 本题考查了等比数列的通项公式及其前n项和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
18.从集合A={1,3,5,7,9}和集合B={2,4,6,8}中各取一个数,那么这两个数之和除3余1的概率是( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{5}$ | C. | $\frac{2}{5}$ | D. | $\frac{3}{10}$ |
15.某几何体三视图如图(单位;cm),则该几何体的体积是( )
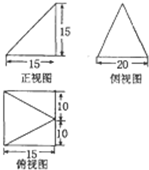

| A. | 1500cm3 | B. | 1025cm3 | C. | 625cm3 | D. | 1200cm3 |