题目内容
10.已知数列{an}和{bn}中,数列{an}的前n项和为Sn,若点(n,Sn)在函数y=-x2的图象上,点(n,bn)在函数y=2x的图象上(1)求数列{an}的通项公式
(2)求数列{anbn}的前n项和Tn.
分析 (1)由点(n,Sn)在函数y=-x2的图象上,可得${S}_{n}=-{n}^{2}$.利用递推式可得当n≥2时,an=Sn-Sn-1.当n=1时,a1=S1,即可得出.
(2)由点(n,bn)在函数y=2x的图象上,可得bn=2n.anbn=(1-2n)•2n.利用“错位相减法”、等比数列的前n项和公式即可得出.
解答 解:(1)∵点(n,Sn)在函数y=-x2的图象上,∴${S}_{n}=-{n}^{2}$.
∴当n≥2时,an=Sn-Sn-1=-n2+(n-1)2=1-2n.当n=1时,a1=S1=-1,符合上式.
∴an=-2n+1.
(2)∵点(n,bn)在函数y=2x的图象上,∴bn=2n.
∴anbn=(1-2n)•2n.
∴Tn=-1×21-3×22-5×23-…-(2n-1)-2n,
∴2Tn=-1×22-3×23-…-(2n-3)×2n-(2n-1)×2n+1.
∴Tn=2+2×22+2×23+…+2×2n+(1-2n)×2n+1=(3-2n)×2n+1-6,
点评 本题考查了等差数列与等比数列的通项公式及其前n项和公式、“错位相减法”、递推式的应用,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
18.从集合A={1,3,5,7,9}和集合B={2,4,6,8}中各取一个数,那么这两个数之和除3余1的概率是( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{5}$ | C. | $\frac{2}{5}$ | D. | $\frac{3}{10}$ |
15.某几何体三视图如图(单位;cm),则该几何体的体积是( )
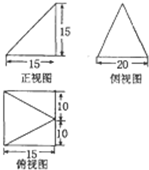

| A. | 1500cm3 | B. | 1025cm3 | C. | 625cm3 | D. | 1200cm3 |
2.在复平面内,复数$\frac{i}{1+i}$+(1+$\sqrt{3}$i)2的共轭复数对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
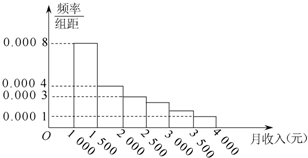 如图是某市有关部门根据该市干部的月收入情况,作抽样调查后画出的样本频率分布直方图.已知图中第一组的频数为4000,请根据该图提供的信息 (图中每组包括左端点,不包括右端点,如第一组表示收入在[1000,1500)),回答:
如图是某市有关部门根据该市干部的月收入情况,作抽样调查后画出的样本频率分布直方图.已知图中第一组的频数为4000,请根据该图提供的信息 (图中每组包括左端点,不包括右端点,如第一组表示收入在[1000,1500)),回答: