题目内容
4.化简:$\frac{sin(-α+180°)-tan(-α)+tan(-α+360°)}{tan(α+180°)+cos(-α)+cos(α+180°)}$.分析 原式利用诱导公式化简,再利用同角三角函数间基本关系变形,约分即可得到结果.
解答 解:原式=$\frac{sinα+tanα-tanα}{tanα+cosα-cosα}$=$\frac{sinα}{\frac{sinα}{cosα}}$=cosα.
点评 此题考查了同角三角函数基本关系的运用,熟练掌握基本关系是解本题的关键.

练习册系列答案
相关题目
15.某几何体三视图如图(单位;cm),则该几何体的体积是( )
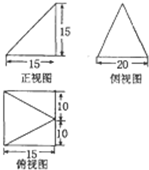

| A. | 1500cm3 | B. | 1025cm3 | C. | 625cm3 | D. | 1200cm3 |
7.下列选项中,说法正确的是( )
| A. | 若命题“p∨q”为真命题,则命题p和命题q均为真命题 | |
| B. | am2<bm2是a<b的必要不充分条件 | |
| C. | x=2kπ+$\frac{π}{4}$(k∈Z)是(-sinx)′=(cosx)′的充要条件 | |
| D. | 命题“若{$\overrightarrow{a}$+$\overrightarrow{b}$,$\overrightarrow{b}$+$\overrightarrow{c}$,$\overrightarrow{c}$+$\overrightarrow{a}$}构成空间的一个基底,则{$\overrightarrow{a}$,$\overrightarrow{b}$$\overrightarrow{c}$}构成空间的一个基底”的否命题为真命题 |
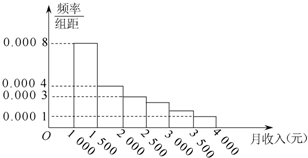 如图是某市有关部门根据该市干部的月收入情况,作抽样调查后画出的样本频率分布直方图.已知图中第一组的频数为4000,请根据该图提供的信息 (图中每组包括左端点,不包括右端点,如第一组表示收入在[1000,1500)),回答:
如图是某市有关部门根据该市干部的月收入情况,作抽样调查后画出的样本频率分布直方图.已知图中第一组的频数为4000,请根据该图提供的信息 (图中每组包括左端点,不包括右端点,如第一组表示收入在[1000,1500)),回答: