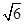题目内容
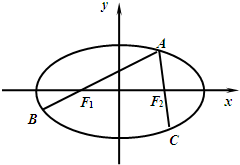
已知点A是椭圆
+
=1(a>b>0)上一点,F为椭圆的一个焦点,且AF⊥x轴,|AF|=焦距,则椭圆的离心率是( )
| x2 |
| a2 |
| y2 |
| b2 |
A.
| B.
| C.
| D.
|
设F为椭圆的右焦点,且AF⊥x轴,所以F(c,0),则
+
=1,解得y=±
,
因为,|AF|=焦距,所以
=2c,即b2=2ac,a2-c2=2ac,
∴e2+2e-1=0,解得e=
-1或e=-
-1(舍去)
故选C.
| c2 |
| a2 |
| y2 |
| b2 |
| b2 |
| a |
因为,|AF|=焦距,所以
| b2 |
| a |
∴e2+2e-1=0,解得e=
| 2 |
| 2 |
故选C.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
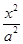 -y2=1交于A、B两点,点F是抛物线的焦点,若△FAB为直角三角形,则该双曲线的离心率为( )
-y2=1交于A、B两点,点F是抛物线的焦点,若△FAB为直角三角形,则该双曲线的离心率为( )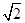 B.
B.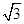 C.2 D.
C.2 D.