题目内容
【题目】在四棱锥
中，
平面ABCD，
，
，
，
.
（1）求证：
平面PAD；
（2）若E是PC的中点，求直线BE与平面PAD所成角的正切值.
【答案】（1）证明见解析.（2）
【解析】
（1）利用线面垂直的判定定理证明即可；（2）利用线面角的定义求解即可.
（1）证明：取
的中点
，连接
，如图，
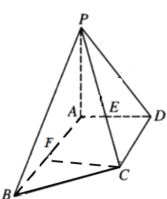
则
//
∴四边形
是平行四边形，
∴
.又∵
，
，
∴
，
又∵
，∴
，
又
平面
，∴
，
∵
平面
，
，
∴
平面.
（2）取
的中点
，靠近
点的四等分点
，连接
，
，
，如图所示，
∵//
//
//
，
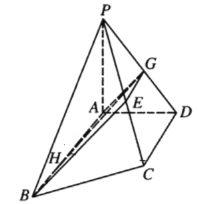
∴四边形
是平行四边形，∴
，
∴直线
与平面所成的角即为直线
与平面所成的角.
∵平面，
∴
即为直线与平面所成的角.
在
中，
，
，
∴
，
即直线与平面所成角的正切值为
本题主要考查了线面垂直的判定性质，线面角的求法，考查了推理论证能力，属于中档题.
练习册系列答案
相关题目
