题目内容
16.在等差数列{an}中,a9=$\frac{1}{2}$a12+6,则该数列的前11项和为( )| A. | 12 | B. | 72 | C. | 132 | D. | 192 |
分析 由已知求得a6,再由S11=11a6求得答案.
解答 解:由a9=$\frac{1}{2}$a12+6,得2a9-a12=12,
即2a1+16d-a1-11d=12,∴a1+5d=12,a6=12.
则S11=11a6=11×12=132.
故选:C.
点评 本题考查等差数列的通项公式,考查了等差数列的前n项和,是基础的计算题.

练习册系列答案
相关题目
8.已知函数①f(x)=x+1;②f(x)=2x-2;③f(x)=$\frac{1}{x}$;④f(x)=lnx;⑤f(x)=cosx;其中对于f(x)定义域内的任意x1,都存在x2,使得f(x1)f(x2)=-x1x2成立的函数是( )
| A. | ①③ | B. | ②⑤ | C. | ③⑤ | D. | ②④ |
5.$\frac{\frac{1}{2}-si{n}^{2}25°}{cos20°•cos70°}$=( )
| A. | $\frac{\sqrt{3}}{4}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{1}{2}$ | D. | 1 |
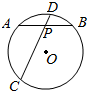 如图,在半径为$\sqrt{7}$的⊙O中,弦AB、CD相交于点P,PA=PB=2,PD=1.
如图,在半径为$\sqrt{7}$的⊙O中,弦AB、CD相交于点P,PA=PB=2,PD=1.
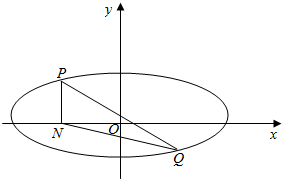 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{{\sqrt{3}}}{2}$,且椭圆C经过点(0,1).
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{{\sqrt{3}}}{2}$,且椭圆C经过点(0,1).