题目内容
已知椭圆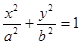
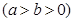 的离心率
的离心率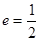 ,右焦点为
,右焦点为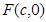 ,方程
,方程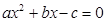 的两个实根
的两个实根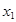 ,
,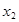 ,则点
,则点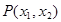 ( )
( )
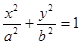
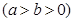 的离心率
的离心率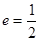 ,右焦点为
,右焦点为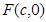 ,方程
,方程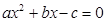 的两个实根
的两个实根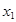 ,
,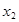 ,则点
,则点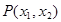 ( )
( )A.必在圆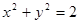 内 内 | B.必在圆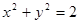 上 上 |
C.必在圆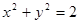 外 外 | D.以上三种情况都有可能 |
A
试题分析:本题只要判断
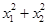 与2的大小,
与2的大小,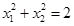 时,点
时,点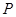 在圆上;
在圆上;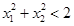 时,点
时,点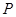 在圆内;
在圆内;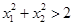 时,点
时,点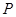 在圆外.由已知
在圆外.由已知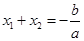 ,
, ,椭圆离心率为
,椭圆离心率为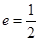 ,从而
,从而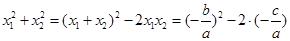
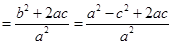
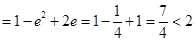 ,点
,点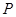 在圆
在圆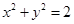 内,故选A.
内,故选A.
练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
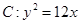 ,点
,点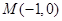 ,过
,过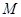 的直线
的直线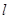 交抛物线
交抛物线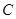 于
于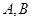 两点.
两点.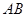 中点的横坐标等于
中点的横坐标等于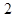 ,求直线
,求直线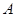 关于
关于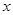 轴的对称点为
轴的对称点为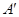 ,求证:直线
,求证:直线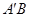 过定点.
过定点. 的椭圆
的椭圆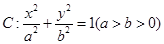 一个焦点为
一个焦点为 .
. 的方程;
的方程;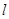 交椭圆
交椭圆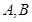 两点,且
两点,且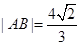 ,求直线
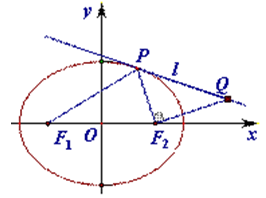
,求直线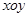 中,已知
中,已知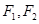 分别是椭圆
分别是椭圆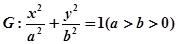 的左、右焦点,椭圆
的左、右焦点,椭圆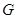 与抛物线
与抛物线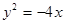 有一个公共的焦点,且过点
有一个公共的焦点,且过点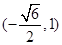 .
.
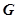 的方程;
的方程;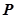 是椭圆
是椭圆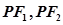 ,过
,过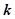 的直线
的直线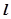 ,使得
,使得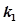 ,
,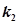 ,试证明
,试证明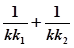 为定值,并求出这个定值;
为定值,并求出这个定值;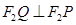 ,设
,设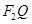 交
交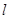 于点
于点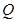 ,
,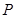 在椭圆上移动时,点
在椭圆上移动时,点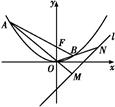
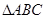 中,
中,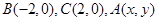 ,给出
,给出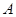 的轨迹方程,下表给出了一些条件及方程:
的轨迹方程,下表给出了一些条件及方程: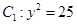
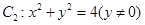
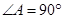
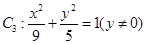
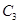 、
、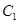 、
、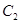 B.
B. 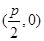 (p为常数,p>0),B为x轴负半轴上的一个动点,动点M使得|AM|=|AB|,且线段BM的中点G在y轴上.
(p为常数,p>0),B为x轴负半轴上的一个动点,动点M使得|AM|=|AB|,且线段BM的中点G在y轴上.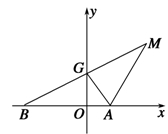
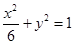 共焦点,且渐近线为
共焦点,且渐近线为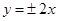 的双曲线方程是( )
的双曲线方程是( )

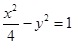
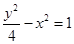
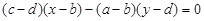 与曲线
与曲线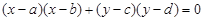 的交点个数是 .
的交点个数是 .