题目内容
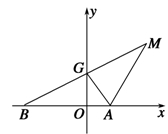
已知定点A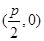 (p为常数,p>0),B为x轴负半轴上的一个动点,动点M使得|AM|=|AB|,且线段BM的中点G在y轴上.
(p为常数,p>0),B为x轴负半轴上的一个动点,动点M使得|AM|=|AB|,且线段BM的中点G在y轴上.
(1)求动点M的轨迹C的方程;
(2)设EF为曲线C的一条动弦(EF不垂直于x轴),其垂直平分线与x轴交于点T(4,0),当p=2时,求|EF|的最大值.
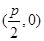 (p为常数,p>0),B为x轴负半轴上的一个动点,动点M使得|AM|=|AB|,且线段BM的中点G在y轴上.
(p为常数,p>0),B为x轴负半轴上的一个动点,动点M使得|AM|=|AB|,且线段BM的中点G在y轴上.
(1)求动点M的轨迹C的方程;
(2)设EF为曲线C的一条动弦(EF不垂直于x轴),其垂直平分线与x轴交于点T(4,0),当p=2时,求|EF|的最大值.
(1)y2=2px(p>0,x≠0)(2)6.
(1)设M(x,y),则BM的中点G的坐标为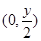 ,B(-x,0).
,B(-x,0).
又A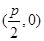 ,故
,故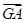 =
=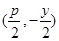 ,
,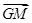 =
=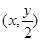 .
.
由题意知GA⊥GM,所以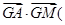 =0,
=0,
即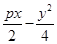 =0,所以y2=2px.
=0,所以y2=2px.
因为M点不能在x轴上,故曲线C的方程为y2=2px(p>0,x≠0).
(2)设弦EF所在直线方程为
y=kx+b,E(x1,y1),F(x2,y2).
由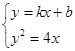 得k2x2+(2kb-4)x+b2=0,①
得k2x2+(2kb-4)x+b2=0,①
则x1+x2=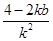 ,x1x2=
,x1x2=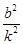 .则线段EF的中点为
.则线段EF的中点为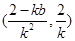 ,线段EF的垂直平分线的方程为:
,线段EF的垂直平分线的方程为:
y-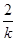 =-
=-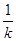
 .令y=0,x=4,得-
.令y=0,x=4,得-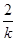 =-
=-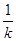
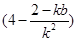 .
.
得bk=2-2k2.所以|EF|2=(1+k2)·(x1-x2)2=(1+k2)·[(x1+x2)2-4x1x2]=(1+k2)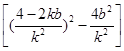 =16(1+k2)·
=16(1+k2)·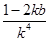 =16(1+k2)·
=16(1+k2)·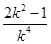 =16
=16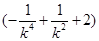 =-16
=-16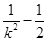 2+36.
2+36.
由①,Δ=(2kb-4)2-4k2b2=4k2b2-16kb+16-4k2b2=16-16kb=16-16(2-2k2)=32k2-16>0.
得k2>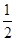 ,即0<
,即0<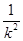 <2.
<2.
所以,当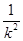 =
=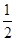 ,即k=±
,即k=±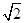 时,|EF|2取得最大值,最大值等于36,即|EF|的最大值为6.
时,|EF|2取得最大值,最大值等于36,即|EF|的最大值为6.
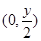 ,B(-x,0).
,B(-x,0).又A
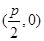 ,故
,故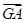 =
=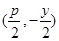 ,
,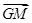 =
=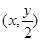 .
.由题意知GA⊥GM,所以
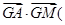 =0,
=0,即
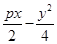 =0,所以y2=2px.
=0,所以y2=2px.因为M点不能在x轴上,故曲线C的方程为y2=2px(p>0,x≠0).
(2)设弦EF所在直线方程为
y=kx+b,E(x1,y1),F(x2,y2).
由
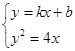 得k2x2+(2kb-4)x+b2=0,①
得k2x2+(2kb-4)x+b2=0,①则x1+x2=
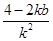 ,x1x2=
,x1x2=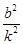 .则线段EF的中点为
.则线段EF的中点为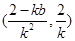 ,线段EF的垂直平分线的方程为:
,线段EF的垂直平分线的方程为:y-
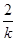 =-
=-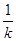
 .令y=0,x=4,得-
.令y=0,x=4,得-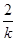 =-
=-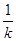
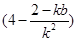 .
.得bk=2-2k2.所以|EF|2=(1+k2)·(x1-x2)2=(1+k2)·[(x1+x2)2-4x1x2]=(1+k2)
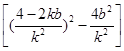 =16(1+k2)·
=16(1+k2)·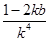 =16(1+k2)·
=16(1+k2)·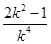 =16
=16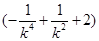 =-16
=-16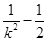 2+36.
2+36.由①,Δ=(2kb-4)2-4k2b2=4k2b2-16kb+16-4k2b2=16-16kb=16-16(2-2k2)=32k2-16>0.
得k2>
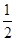 ,即0<
,即0<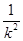 <2.
<2.所以,当
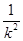 =
=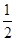 ,即k=±
,即k=±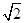 时,|EF|2取得最大值,最大值等于36,即|EF|的最大值为6.
时,|EF|2取得最大值,最大值等于36,即|EF|的最大值为6.
练习册系列答案
相关题目
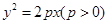 的焦点为
的焦点为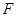 ,点
,点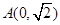 ,线段
,线段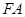 的中点在抛物线上.设动直线
的中点在抛物线上.设动直线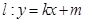 与抛物线相切于点
与抛物线相切于点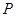 ,且与抛物线的准线相交于点
,且与抛物线的准线相交于点 ,以
,以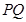 为直径的圆记为圆
为直径的圆记为圆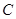 .
.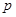 的值;
的值;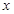 轴的位置关系;
轴的位置关系;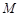 ,使得圆
,使得圆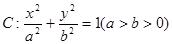 的离心率为
的离心率为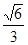 ,短轴一个端点到右焦点的距离为
,短轴一个端点到右焦点的距离为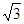 .
.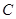 的方程;
的方程;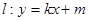 与椭圆
与椭圆 两点,坐标原点
两点,坐标原点 到直线
到直线 的距离为
的距离为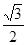 ,求
,求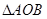 面积的最大值.
面积的最大值.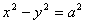 (其中
(其中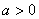 ).
).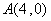 到双曲线上的点的最近距离为
到双曲线上的点的最近距离为 ,求
,求 的值;
的值; ,作倾斜角为
,作倾斜角为 的直线
的直线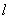 交双曲线于
交双曲线于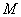 、
、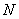 两点,其中
两点,其中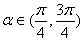 ,
,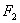 是双曲线的右焦点.求△
是双曲线的右焦点.求△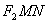 的面积
的面积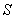 .
.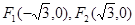 ,曲线C是使
,曲线C是使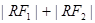 为定值的点
为定值的点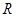 的轨迹,曲线
的轨迹,曲线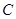 过点
过点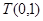 .
.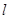 过点
过点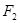 ,且与曲线
,且与曲线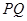 ,当
,当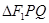 的面积取得最大值时,求直线
的面积取得最大值时,求直线 是曲线
是曲线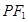 、
、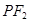 ,设
,设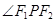 的角平分线
的角平分线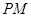 交曲线
交曲线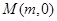 ,求
,求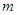 的取值范围.
的取值范围. 中,已知点
中,已知点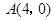 ,动点
,动点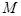 在
在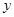 轴上的正射影为点
轴上的正射影为点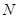 ,且满足直线
,且满足直线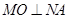 .
.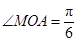 时,求直线
时,求直线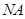 的方程.
的方程.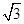 ,1)到两焦点的距离之和为4
,1)到两焦点的距离之和为4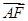 =3
=3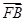 .求过O,A,B三点的圆的方程.
.求过O,A,B三点的圆的方程.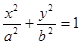
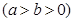 的离心率
的离心率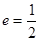 ,右焦点为
,右焦点为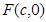 ,方程
,方程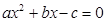 的两个实根
的两个实根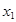 ,
,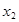 ,则点
,则点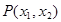 ( )
( ) 内
内 的焦点
的焦点 到准线
到准线 的距离是 .
的距离是 .