题目内容
【题目】已知两定点![]() ,点
,点![]() 是平面内的动点,且
是平面内的动点,且![]() ,记
,记![]() 的轨迹是
的轨迹是![]()
(1)求曲线![]() 的方程;
的方程;
(2)过点![]() 引直线
引直线![]() 交曲线
交曲线![]() 于
于![]() 两点,设
两点,设![]() ,点
,点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,证明直线
,证明直线![]() 过定点.
过定点.
【答案】(1)![]() ;(2)见解析
;(2)见解析
【解析】
设![]() ,根据条件列方程化简即可;(2)先探究特殊性,当点Q为椭圆的上顶
,根据条件列方程化简即可;(2)先探究特殊性,当点Q为椭圆的上顶
点(0,![]() )时,直线RN过定点P(4,0).再讨论一般情形,设直线l:
)时,直线RN过定点P(4,0).再讨论一般情形,设直线l:![]() 点R,N,P三点共线,因此直线RN经过定点P(4,0).
点R,N,P三点共线,因此直线RN经过定点P(4,0).
(1)设![]() ,
,![]() ,
,![]() ,
,
则![]() ,
,![]() ,
,
由于![]() ,
,
即![]() ,设
,设![]() ,
,![]() ,
,
则![]() ,点
,点![]() 的轨迹是以
的轨迹是以![]() ,
,![]() 为焦点的椭圆,
为焦点的椭圆,
故![]() ,
,![]() ,
,![]() ,
,
所以,动点![]() 的轨迹
的轨迹![]() 的方程为:
的方程为:![]() .
.
如图所示,

先探究特殊性,当点Q为椭圆的上顶点(0,![]() )时,直线l:
)时,直线l:![]() ,
,
联立直线和椭圆方程得![]() ,
,
![]() 直线RN:
直线RN:![]() 令y=0,得x=4,
令y=0,得x=4,
所以直线RN过定点P(4,0).
下面证明一般情形:
设直线l:![]()
联立![]() ,
,
判别式![]()
所以![]()
![]()
即![]() ,
,
设![]() ,于是,
,于是,
 ,
,
又![]() ,
,
解得![]() ,
,
所以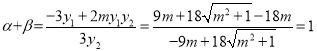 ,
,
所以点R,N,P三点共线,因此直线RN经过定点P(4,0).
综上,直线RN经过定点P(4,0).

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目