题目内容
【题目】在直三棱柱![]() 中,
中,![]() ,
,![]() ,D为线段AC的中点.
,D为线段AC的中点.
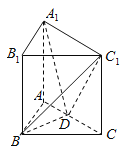
(1)求证:![]() :
:
(2)求直线![]() 与平面
与平面![]() 所成角的余弦值;
所成角的余弦值;
(3)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析;(2)![]() ;(3)
;(3)![]()
【解析】
(1)由直三棱柱的定义可得![]() ,再根据等腰三角形性质可得
,再根据等腰三角形性质可得![]() ,再由线面垂直的判定可得
,再由线面垂直的判定可得![]() 平面
平面![]() ,即可证明
,即可证明![]() .
.
(2)取线段![]() 的中点为
的中点为![]() ,分别取
,分别取![]() 作为
作为![]() 轴,
轴,![]() 轴,
轴,![]() 轴,建立空间直角坐标系,写出各个点的坐标,利用向量数量积运算求得平面BC1D的法向量,即可由线面夹角的求法求得直线
轴,建立空间直角坐标系,写出各个点的坐标,利用向量数量积运算求得平面BC1D的法向量,即可由线面夹角的求法求得直线![]() 与平面
与平面![]() 所成角的余弦值.
所成角的余弦值.
(3)由平面BC1D的法向量和平面![]() 的法向量,即可利用法向量法求得二面角
的法向量,即可利用法向量法求得二面角![]() 的余弦值.
的余弦值.
(1)证明:由直三棱柱![]() ,可得
,可得![]() 底面
底面![]() ,
,
∴![]() .
.
∵![]() ,D为线段
,D为线段![]() 的中点.
的中点.
∴![]() ,又
,又![]() ,
,
∴![]() 平面
平面![]() ,
,
∴![]() .
.
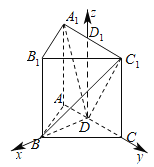
(2)取线段![]() 的中点为
的中点为![]() ,分别取
,分别取![]() 作为
作为![]() 轴,
轴,![]() 轴,
轴,![]() 轴,建立空间直角坐标系,如下图所示:
轴,建立空间直角坐标系,如下图所示:
![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
设平面BC1D的法向量为![]() ,
,
则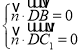 ,代入可得
,代入可得![]() ,令
,令![]() 可得
可得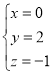
即![]() .
.
∴直线![]() 与平面
与平面![]() 所成角的余弦值
所成角的余弦值
|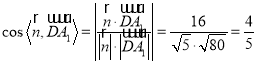 |.
|.
(3)![]() ,
,![]() ,
,![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,
,
则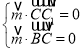 ,代入可得
,代入可得![]() ,令
,令![]() ,解得
,解得![]()
即![]() .
.
∴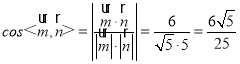 .
.
由图可知,二面角![]() 为锐二面角
为锐二面角
∴二面角![]() 的余弦值为
的余弦值为![]() .
.

练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目