��Ŀ����
����Ŀ��ר���о�������![]() 2.5��������Ҫ�ɷݣ����о�
2.5��������Ҫ�ɷݣ����о�![]() 2.5�γ�ԭ��ʱ��ij�о���Ա�о���
2.5�γ�ԭ��ʱ��ij�о���Ա�о���![]() 2.5��ȼ���ŷŵ�
2.5��ȼ���ŷŵ�![]() ��
��![]() ��
��![]() ��
��![]() �����ʵ���ع�ϵ.��ͼ��ij��ij��
�����ʵ���ع�ϵ.��ͼ��ij��ij��![]() 2.5��
2.5��![]() ��
��![]() ����Ե�ɢ��ͼ.
����Ե�ɢ��ͼ.
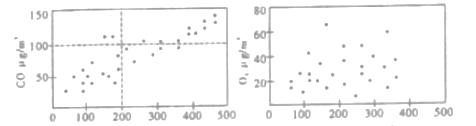
����������ɢ��ͼ�������![]() ��
��![]() ��
��![]() 2.5��Ӱ���ϵ�����������ۣ�
2.5��Ӱ���ϵ�����������ۣ�
�������йع涨����![]() �ŷ�������
�ŷ�������![]() ʱ
ʱ![]() �ŷ�����꣬��֮Ϊ
�ŷ�����꣬��֮Ϊ![]() �ŷ������ꣻ��
�ŷ������ꣻ��![]() 2.5ֵ����
2.5ֵ����![]() ʱ�������أ���֮����������.����
ʱ�������أ���֮����������.����![]() 2.5��
2.5��![]() ����Ե�ɢ��ͼ��д������
����Ե�ɢ��ͼ��д������![]() �����������ж��ж��İ�����Ϊ�������Ƿ��������ŷ����йء���
�����������ж��ж��İ�����Ϊ�������Ƿ��������ŷ����йء���
���������� | �������� | �ܼ� | |
| |||
| |||
�ܼ� |
��������֪�������Խ�ͨӰ��ϴ�.ij�н�ͨ���ŷ��֣���һ�����ڣ���![]() �ŷ����ֱ���60��120,180ʱ��ij·�ڵĽ�ͨ��������λ��������һ����800��600,200������һ�����ڣ�
�ŷ����ֱ���60��120,180ʱ��ij·�ڵĽ�ͨ��������λ��������һ����800��600,200������һ�����ڣ�![]() �ŷ�����60,120,180�ĸ���һ����
�ŷ�����60,120,180�ĸ���һ����![]() ��
��![]() ��
��![]() ��
��![]() �������·��һ���µĽ�ͨ��������ֵ��ȡֵ��Χ.
�������·��һ���µĽ�ͨ��������ֵ��ȡֵ��Χ.
����
0.100 | 0.050 | 0.010 | 0.001 | |
2.706 | 3.841 | 6.635 | 10.828 |
![]()
���𰸡�����![]() ��
��![]() ������ع�ϵ����
������ع�ϵ����![]() ��
��![]() û����ع�ϵ��������������������.
û����ع�ϵ��������������������.
�������������������������ͼ��ɢ��ֲ���һ�����������ڣ��ɵ�![]() ��
��![]() ��������ع�ϵ������ͼɢ��֮��ֲ���ɢ�����н�ǿ����ع�ϵ��������ɢ��ͼ����������������
��������ع�ϵ������ͼɢ��֮��ֲ���ɢ�����н�ǿ����ع�ϵ��������ɢ��ͼ����������������![]() ��ֵ�����жϽ���������ݸ��ʺ�Ϊ
��ֵ�����жϽ���������ݸ��ʺ�Ϊ![]() ��
��![]() ��
��![]() ��ʾ�����������ֵ����
��ʾ�����������ֵ����![]() �ķ�Χ�õ������ķ�Χ.
�ķ�Χ�õ������ķ�Χ.
�������������![]() ��
��![]() ������ع�ϵ����
������ع�ϵ����![]() ��
��![]() û����ع�ϵ.
û����ع�ϵ.
�������������£�
���������� | �������� | �ܼ� | |
| 13 | 5 | 18 |
| 2 | 10 | 12 |
�ܼ� | 15 | 15 | 30 |
�ɱ������ݿ�֪![]()
![]() .
.
����99.5%�İ�����Ϊ�������Ƿ�������![]() �ŷ����йء�.
�ŷ����йء�.
�����轻ͨ������![]() ��������·ֲ��У�
��������·ֲ��У�
��ͨ���� | 800 | 600 | 200 |
|
|
|
|
��Ϊ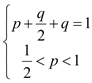 ������
������![]()
![]() .
.
��![]() ������ͨ��������ֵ��566.7������800����֮��.
������ͨ��������ֵ��566.7������800����֮��.

����Ŀ������ͳ��ѧ�ķ�չ��Դ�ڶ�ʮ���ͳ��������ڸ����۵Ļ����Ϸ�չ������,ͳ�����ʵĹ��������ݵ�Զ�ŵġ��������¡��͡���ʮ��ʷ���д����Ĺ������˿ڡ�Ǯ���� ˮ�ġ����ġ���������ϵļ�¼.�����꣬������Ϯ����ij�и���11�·ݵ������������ͳ�ƣ�������£���һ
���� |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
���� | �� | �� | �� | �� | �� | �� | �� | �� | �� | �� | �� | �� | �� | �� | �� |
���� |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
���� | �� | �� | �� | �� | �� | �� | �� | �� | �� | �� | �� | �� | �� | �� | �� |
���ڴ������ij������Ϊ���������ڴ����ȡ��ȫ�����е�����.
�±���һ�����˻����Ա���������11�·ݣ����겻����![]() �졢��������
�졢��������![]() �칲
�칲![]() �죩�ĵ�������
�죩�ĵ�������
����
������ | ���� | �ܼ� | |
û������ |
| ||
������ |
| ||
�ܼ� |
|
|
|
(1)���ɱ�һ������![]() �������ڸ���11�·���ȡһ�죬���Ƹ���������ĸ��ʣ�
�������ڸ���11�·���ȡһ�죬���Ƹ���������ĸ��ʣ�
(2)����ͳ��ѧԭ��������û��![]() �İ�����Ϊ�����������й�ϵ��������ʱ�ж�����û��������
�İ�����Ϊ�����������й�ϵ��������ʱ�ж�����û��������
(���ڲ���ʹ�ü����������Ա�������ʹ��ʱ��������ȡ����)
|
|
|
|
|
|
|
|
|
|