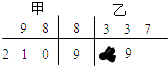题目内容
【题目】已知定义域为R的函数 ![]() 是奇函数.
是奇函数.
(1)求实数a,b的值;
(2)判断f(x)在(﹣∞,+∞)上的单调性;
(3)若f(k3x)+f(3x﹣9x+2)>0对任意x≥1恒成立,求k的取值范围.
【答案】
(1)解:f(x)在R上为奇函数;
∴ ![]() ;
;
∴ 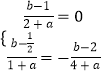 ;
;
解得a=2,b=1
(2)解: ![]() ;
;
x增大时,2x+1增大, ![]() 减小,f(x)减小;
减小,f(x)减小;
∴f(x)在(﹣∞,+∞)上单调递减
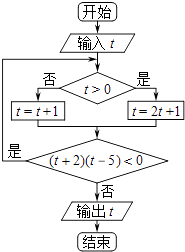
(3)解:∵f(x)为奇函数,∴由f(k3x)+f(3x﹣9x+2)>0得,f(k3x)>f(9x﹣3x﹣2);
又f(x)在(﹣∞,+∞)上单调递减;
∴k3x<9x﹣3x﹣2,该不等式对于任意x≥1恒成立;
∴(3x)2﹣(k+1)3x﹣2>0对任意x≥1恒成立;
设3x=t,则t2﹣(k+1)t﹣2>0对于任意t≥3恒成立;
设g(t)=t2﹣(k+1)t﹣2,△=(k+1)2+8>0;
∴k应满足: 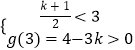 ;
;
解得 ![]() ;
;
∴k的取值范围为 ![]()
【解析】(1)根据f(x)为R上的奇函数便可得到 ![]() ,这样便可求出a=2,b=1;(2)分离常数可以得到
,这样便可求出a=2,b=1;(2)分离常数可以得到 ![]() ,根据指数函数y=2x的单调性可以判断出x增大时,f(x)减小,从而可判断出f(x)在(﹣∞,+∞)上单调递减;(3)根据f(x)的奇偶性和单调性便可由f(k3x)+f(3x﹣9x+2)>0得到(3x)2﹣(k+1)3x﹣2>0对于任意的x≥1恒成立,可设3x=t,从而有t2﹣(k+1)t﹣2>0对于任意的t≥3恒成立,可设g(t)=t2﹣(k+1)t﹣2,从而可以得到
,根据指数函数y=2x的单调性可以判断出x增大时,f(x)减小,从而可判断出f(x)在(﹣∞,+∞)上单调递减;(3)根据f(x)的奇偶性和单调性便可由f(k3x)+f(3x﹣9x+2)>0得到(3x)2﹣(k+1)3x﹣2>0对于任意的x≥1恒成立,可设3x=t,从而有t2﹣(k+1)t﹣2>0对于任意的t≥3恒成立,可设g(t)=t2﹣(k+1)t﹣2,从而可以得到 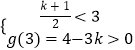 ,这样解该不等式组便可得出k的取值范围.
,这样解该不等式组便可得出k的取值范围.
【考点精析】本题主要考查了函数单调性的判断方法和函数的奇偶性的相关知识点,需要掌握单调性的判定法:①设x1,x2是所研究区间内任两个自变量,且x1<x2;②判定f(x1)与f(x2)的大小;③作差比较或作商比较;偶函数的图象关于y轴对称;奇函数的图象关于原点对称才能正确解答此题.

 通城学典默写能手系列答案
通城学典默写能手系列答案【题目】专家研究表明,![]() 2.5是霾的主要成份,在研究
2.5是霾的主要成份,在研究![]() 2.5形成原因时,某研究人员研究了
2.5形成原因时,某研究人员研究了![]() 2.5与燃烧排放的
2.5与燃烧排放的![]() 、
、![]() 、
、![]() 、
、![]() 等物质的相关关系.下图是某地某月
等物质的相关关系.下图是某地某月![]() 2.5与
2.5与![]() 和
和![]() 相关性的散点图.
相关性的散点图.
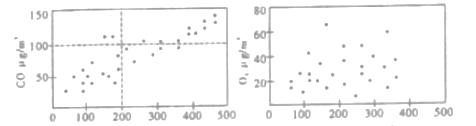
(Ⅰ)根据上面散点图,请你就![]() ,
,![]() 对
对![]() 2.5的影响关系做出初步评价;
2.5的影响关系做出初步评价;
(Ⅱ)根据有关规定,当![]() 排放量低于
排放量低于![]() 时
时![]() 排放量达标,反之为
排放量达标,反之为![]() 排放量超标;当
排放量超标;当![]() 2.5值大于
2.5值大于![]() 时雾霾严重,反之雾霾不严重.根据
时雾霾严重,反之雾霾不严重.根据![]() 2.5与
2.5与![]() 相关性的散点图填写好下面
相关性的散点图填写好下面![]() 列联表,并判断有多大的把握认为“雾霾是否严重与排放量有关”:
列联表,并判断有多大的把握认为“雾霾是否严重与排放量有关”:
雾霾不严重 | 雾霾严重 | 总计 | |
| |||
| |||
总计 |
(Ⅲ)我们知道雾霾对交通影响较大.某市交通部门发现,在一个月内,当![]() 排放量分别是60,120,180时,某路口的交通流量(单位:万辆)一次是800,600,200,而在一个月内,
排放量分别是60,120,180时,某路口的交通流量(单位:万辆)一次是800,600,200,而在一个月内,![]() 排放量是60,120,180的概率一次是
排放量是60,120,180的概率一次是![]() ,
,![]() ,
,![]() (
(![]() ),求该路口一个月的交通流量期望值的取值范围.
),求该路口一个月的交通流量期望值的取值范围.
附:
0.100 | 0.050 | 0.010 | 0.001 | |
2.706 | 3.841 | 6.635 | 10.828 |
![]()