题目内容
【题目】给出下列四个命题:
①函数y=|x|与函数y= ![]() 表示同一个函数;
表示同一个函数;
②奇函数的图象一定通过直角坐标系的原点;
③函数y=3(x﹣1)2的图象可由y=3x2的图象向右平移1个单位得到;
④若函数f(x)的定义域为[0,2],则函数f(2x)的定义域为[0,4];
⑤设函数f(x)是在区间[a.b]上图象连续的函数,且f(a)f(b)<0,则方程f(x)=0在区间[a,b]上至少有一实根.
其中正确命题的序号是 . (填上所有正确命题的序号)
【答案】③⑤
【解析】解:①函数y=|x|的定义域为R,函数y= ![]() 的定义域为[0,+∞),两函数的定义域不同,不是同一函数,①错误
的定义域为[0,+∞),两函数的定义域不同,不是同一函数,①错误
②函数y= ![]() 为奇函数,但其图象不过坐标原点,②错误
为奇函数,但其图象不过坐标原点,②错误
③将y=3x2的图象向右平移1个单位得到y=3(x﹣1)2的图象,③正确
④∵函数f(x)的定义域为[0,2],要使函数f(2x)有意义,需0≤2x≤2,即x∈[0,1],故函数f(2x)的定义域为[0,1],④错误;
⑤函数f(x)是在区间[a.b]上图象连续的函数,f(a)f(b)<0,则方程f(x)=0在区间[a,b]上至少有一实根,⑤正确;
故答案为 ③⑤
①两函数的定义域不同,不是同一函数,①错误;②举反例如函数y= ![]() ,②错误;③利用函数图象平移变换理论可知③正确;④求函数f(2x)的定义域可判断④错误;⑤由根的存在性定理可判断⑤错误.
,②错误;③利用函数图象平移变换理论可知③正确;④求函数f(2x)的定义域可判断④错误;⑤由根的存在性定理可判断⑤错误.

 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案【题目】专家研究表明,![]() 2.5是霾的主要成份,在研究
2.5是霾的主要成份,在研究![]() 2.5形成原因时,某研究人员研究了
2.5形成原因时,某研究人员研究了![]() 2.5与燃烧排放的
2.5与燃烧排放的![]() 、
、![]() 、
、![]() 、
、![]() 等物质的相关关系.下图是某地某月
等物质的相关关系.下图是某地某月![]() 2.5与
2.5与![]() 和
和![]() 相关性的散点图.
相关性的散点图.
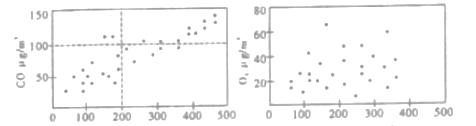
(Ⅰ)根据上面散点图,请你就![]() ,
,![]() 对
对![]() 2.5的影响关系做出初步评价;
2.5的影响关系做出初步评价;
(Ⅱ)根据有关规定,当![]() 排放量低于
排放量低于![]() 时
时![]() 排放量达标,反之为
排放量达标,反之为![]() 排放量超标;当
排放量超标;当![]() 2.5值大于
2.5值大于![]() 时雾霾严重,反之雾霾不严重.根据
时雾霾严重,反之雾霾不严重.根据![]() 2.5与
2.5与![]() 相关性的散点图填写好下面
相关性的散点图填写好下面![]() 列联表,并判断有多大的把握认为“雾霾是否严重与排放量有关”:
列联表,并判断有多大的把握认为“雾霾是否严重与排放量有关”:
雾霾不严重 | 雾霾严重 | 总计 | |
| |||
| |||
总计 |
(Ⅲ)我们知道雾霾对交通影响较大.某市交通部门发现,在一个月内,当![]() 排放量分别是60,120,180时,某路口的交通流量(单位:万辆)一次是800,600,200,而在一个月内,
排放量分别是60,120,180时,某路口的交通流量(单位:万辆)一次是800,600,200,而在一个月内,![]() 排放量是60,120,180的概率一次是
排放量是60,120,180的概率一次是![]() ,
,![]() ,
,![]() (
(![]() ),求该路口一个月的交通流量期望值的取值范围.
),求该路口一个月的交通流量期望值的取值范围.
附:
0.100 | 0.050 | 0.010 | 0.001 | |
2.706 | 3.841 | 6.635 | 10.828 |
![]()