题目内容
20.已知向量$\overrightarrow{a}$=(-1,2x),$\overrightarrow{b}$=(2,2y),且$\overrightarrow{a}$⊥$\overrightarrow{b}$,则|$\overrightarrow{a}$+$\overrightarrow{b}$|的最小值为3.分析 根据$\overrightarrow{a}$⊥$\overrightarrow{b}$,得出xy的值,再利用基本不等式求出$|\overrightarrow a+\overrightarrow b|$的最小值.
解答 解:∵向量$\overrightarrow{a}$=(-1,2x),$\overrightarrow{b}$=(2,2y),且$\overrightarrow{a}$⊥$\overrightarrow{b}$,
∴-1×2+2x•2y=0,
∴xy=$\frac{1}{2}$,
∴$|\overrightarrow a+\overrightarrow b|=\sqrt{1+{{(2x+2y)}^2}}=\sqrt{4({x^2}+{y^2})+5}≥\sqrt{8xy+5}=3$,
∴$|\overrightarrow a+\overrightarrow b|$的最小值为3.
故答案为:3.
点评 本题考查了平面向量的简单应用问题,也考查了有关平面向量模长的计算问题,是基础题目.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
5.函数f(x)=x•e|x|的大致图象为( )
| A. | 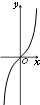 | B. | 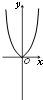 | C. | 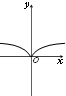 | D. | 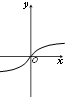 |
10.某设备的使用年限x(单位:年)与所支付的维修费用y(单位:千元)的一组数据如表:
从散点图分析.Y与x线性相关,根据上表中数据可得其线性回归方程:$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$中的$\widehat{b}$=1.54.由此预测该设备的使用年限为6年时需支付的维修费用约是( )
| 使用年限x | 2 | 3 | 4 | 5 |
| 维修费用y | 2 | 3.4 | 5 | 6.6 |
| A. | 7.2千元 | B. | 7.8千元 | C. | 8.1千元 | D. | 9.5千元 |
 ,若
,若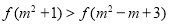 ,则实数
,则实数 的取值范围是( )
的取值范围是( ) B.
B.
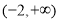 D.
D.
