题目内容
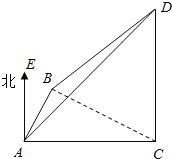
【题目】一个大型喷水池的中央有一个强力喷水柱,为了测量喷水柱喷出的水柱的高度,某人在喷水柱正西方向的点A测得水柱顶端的仰角为45°,沿点A向北偏东30°前进100 m到达点B,在B点测得水柱顶端的仰角为30°,则水柱的高度是( )
A. 50 mB. 100 m
C. 120 mD. 150 m
【答案】A
【解析】
如图所示,设水柱CD的高度为h.在Rt△ACD中,由∠DAC=45°,可得AC=h.由∠BAE=30°,可得∠CAB=60°.在Rt△BCD中,∠CBD=30°,可得BC=![]() .在△ABC中,由余弦定理可得:BC2=AC2+AB2﹣2ACABcos60°.代入即可得出.
.在△ABC中,由余弦定理可得:BC2=AC2+AB2﹣2ACABcos60°.代入即可得出.
如图所示,
设水柱CD的高度为h.
在Rt△ACD中,∵∠DAC=45°,∴AC=h.
∵∠BAE=30°,∴∠CAB=60°.
又∵B,A,C在同一水平面上,∴△BCD是以C为直角顶点的直角三角形,
在Rt△BCD中,∠CBD=30°,∴BC=![]() .
.
在△ABC中,由余弦定理可得:BC2=AC2+AB2﹣2ACABcos60°.
∴(![]() )2=h2+1002﹣
)2=h2+1002﹣![]() ,
,
化为h2+50h﹣5000=0,解得h=50.
故选:A.

 名校课堂系列答案
名校课堂系列答案【题目】某公司要了解某商品的年广告费![]() (单位:万元)对年销售额
(单位:万元)对年销售额![]() (单位:万元)的影响,对近4年的年广告费
(单位:万元)的影响,对近4年的年广告费![]() 和年销售额
和年销售额![]() 数据作了初步调研,得到下面的表格:
数据作了初步调研,得到下面的表格:
年广告费 | 2 | 3 | 4 | 5 |
年销售额 | 26 | 39 | 49 | 54 |
用广告费作解释变量,年销售额作预报变量,且![]() 适宜作为年销售额
适宜作为年销售额![]() 关于年广告费
关于年广告费![]() 的回归方程类型.
的回归方程类型.
(1)根据表中数据,建立![]() 关于
关于![]() 的回归方程.
的回归方程.
(2)已知商品的年利润![]() 与
与![]() ,
,![]() 的关系式为
的关系式为![]() ,根据(1)中的结果,估计年广告费
,根据(1)中的结果,估计年广告费![]() 为何值时(小数点后保留两位),年利润的预报值最大?
为何值时(小数点后保留两位),年利润的预报值最大?
(对于数据![]() ,其回归方程
,其回归方程![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为 ,
,![]() ).
).
【题目】某电子商务公司随机抽取1000名网购者进行调查.这1000名购物者2018年网购金额(单位:万元)均在区间![]() 内,样本分组为:
内,样本分组为:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,购物金额的频率分布直方图如下:
,购物金额的频率分布直方图如下:

电子商务公司决定给购物者发放优惠券,其金额(单位:元)与购物金额关系如下:
购物金额分组 |
|
|
|
|
发放金额 | 50 | 100 | 150 | 200 |
(1)求这1000名购物者获得优惠券金额的平均数;
(2)以这1000名购物者购物金额落在相应区间的频率作为概率,求一个购物者获得优惠券金额不少于150元的概率.