ÌâÄżÄÚÈĘ
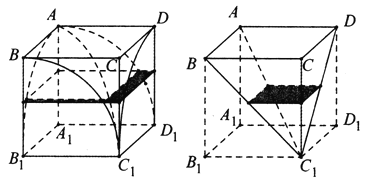
ĄŸÌâÄżĄżÎȘÍÆ”ŒÇò”ÄÌć»ęč«ÊœŁŹÁő»ŐÖÆÔìÁËÒ»žöÄČșÏ·œžÇŁšÔÚÒ»žöŐę·œÌćÄÚŚśÁœžö»„ÏàŽčÖ±”ÄÄÚÇĐÔČÖùŁŹŐâÁœžöÔČÖù”Äč«čČČż·ÖœĐŚöÄČșÏ·œžÇŁ©ŁŹ”«Ă»ÓДÔœÄČșÏ·œžÇ”ÄÌć»ęŁź200ÄêșóŁŹŚæžűłöÄČșÏ·œžÇ”ÄÌć»ęŒÆËă·œ·šŁŹÆäșËĐÄčęłÌ±»șóÈËłÆÎȘŚæÔÀíŁșÔ”ĂĘÊÆŒÈÍŹŁŹÔò»ęČ»ÈĘÒìŁźÒâËŒÊÇŁŹŒĐÔÚÁœžöÆœĐĐÆœĂæŒä”ÄÁœžöŒžșÎÌć±»ÆœĐĐÓÚŐâÁœžöÆœĐĐÆœĂæ”ÄÈÎÒâÆœĂæËùœŰŁŹÈçčûœŰĂæ”ÄĂæ»ęŚÜÏà”ÈŁŹÄÇĂŽŐâÁœžöŒžșÎÌć”ÄÌć»ęÒČÏà”ÈŁźÏÖÔÚœŰÈĄÄČșÏ·œžÇ”Ä°Ë·ÖÖźÒ»ŁŹËü”ÄÍâÇĐŐę·œÌć![]() ”ÄÀⳀÎȘ1ŁŹÈçÍŒËùÊŸŁŹžùŸĘÒÔÉÏĐĆÏąŁŹÔòžĂÄČșÏ·œžÇ”ÄÌć»ęÎȘŁš Ł©
”ÄÀⳀÎȘ1ŁŹÈçÍŒËùÊŸŁŹžùŸĘÒÔÉÏĐĆÏąŁŹÔòžĂÄČșÏ·œžÇ”ÄÌć»ęÎȘŁš Ł©
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
ĄŸŽđ°žĄżB
ĄŸœâÎöĄż·ÖÎöŁșÔڞ߶È![]() ŽŠ”ÄœŰĂæŁŹÓĂÆœĐĐÓëŐę·œÌćÉÏÏ”ŚĂæ”ÄÆœĂæÈ„œŰŁŹŒÇœŰ”ĂÁœÔČÖùÌćč«čČČż·ÖËù”ĂĂæ»ęÎȘ
ŽŠ”ÄœŰĂæŁŹÓĂÆœĐĐÓëŐę·œÌćÉÏÏ”ŚĂæ”ÄÆœĂæÈ„œŰŁŹŒÇœŰ”ĂÁœÔČÖùÌćč«čČČż·ÖËù”ĂĂæ»ęÎȘ![]() ŁŹœŰ”ĂŐę·œÌćËù”ĂĂæ»ęÎȘ
ŁŹœŰ”ĂŐę·œÌćËù”ĂĂæ»ęÎȘ![]() ŁŹœâ”ĂŚ”ÌćËù”ĂĂæ»ęÎȘ
ŁŹœâ”ĂŚ”ÌćËù”ĂĂæ»ęÎȘ![]() ŁŹ
ŁŹ![]() ŁŹ
ŁŹ
![]() ŁŹÇółö
ŁŹÇółö![]() ŁŹÔÙÓɶš»ę·ÖÇółöŚ¶ÌćÌć»ęŁŹÓÉŐę·œÌć”ÄÌć»ęŒőÈ„Ś¶ÌćÌć»ęŒŽżÉ.
ŁŹÔÙÓɶš»ę·ÖÇółöŚ¶ÌćÌć»ęŁŹÓÉŐę·œÌć”ÄÌć»ęŒőÈ„Ś¶ÌćÌć»ęŒŽżÉ.
ÏêœâŁșÔڞ߶È![]() ŽŠ”ÄœŰĂæŁŹÓĂÆœĐĐÓëŐę·œÌćÉÏÏ”ŚĂæ”ÄÆœĂæÈ„œŰŁŹ
ŽŠ”ÄœŰĂæŁŹÓĂÆœĐĐÓëŐę·œÌćÉÏÏ”ŚĂæ”ÄÆœĂæÈ„œŰŁŹ
ŒÇœŰ”ĂÁœÔČÖùÌćč«čČČż·ÖËù”ĂĂæ»ęÎȘ![]() ŁŹœŰ”ĂŐę·œÌćËù”ĂĂæ»ęÎȘ
ŁŹœŰ”ĂŐę·œÌćËù”ĂĂæ»ęÎȘ![]() ŁŹ
ŁŹ
żÉ”Ă![]() ŁŹ
ŁŹ![]() ŁŹ
ŁŹ
ÓÉ![]() ŁŹżÉ”Ă
ŁŹżÉ”Ă![]() ŁŹÔò
ŁŹÔò![]() ŁŹ
ŁŹ
ËùÒÔžĂÄČșÏ·œžÇ”ÄÌć»ęÎȘ![]() ŁŹčÊŃĄB.
ŁŹčÊŃĄB.

ĄŸÌâÄżĄżËæŚĆÉç»á”Ä·ąŐ裏ÖŐÉíŃ§Ï°łÉÎȘ±ŰÒȘŁŹč€ÈËÖȘʶÒȘžüĐÂŁŹŃ§Ï°ĆàŃ”±ŰČ»żÉÉÙŁŹÏÖij耳§ÓĐč€ÈË1000ĂûŁŹÆäÖĐ250Ăûč€ÈËČΌӶÌÆÚĆàŃ”ŁšłÆÎȘ![]() Ààč€ÈËŁ©ŁŹÁíÍâ750Ăûč€ÈËČÎŒÓč곀ÆÚĆàŃ”ŁšłÆÎȘ
Ààč€ÈËŁ©ŁŹÁíÍâ750Ăûč€ÈËČÎŒÓč곀ÆÚĆàŃ”ŁšłÆÎȘ![]() Ààč€ÈËŁ©ŁŹŽÓžĂ耳§”Äč€ÈËÖĐčČłéČéÁË100Ăûč€ÈËŁŹ”śČéËûĂÇ”ÄÉúČúÄÜÁŠŁšŽËŽŠÉúČúÄÜÁŠÖžÒ»ÌìŒÓ耔ÄÁăŒțÊ꣩”Ă”œ
Ààč€ÈËŁ©ŁŹŽÓžĂ耳§”Äč€ÈËÖĐčČłéČéÁË100Ăûč€ÈËŁŹ”śČéËûĂÇ”ÄÉúČúÄÜÁŠŁšŽËŽŠÉúČúÄÜÁŠÖžÒ»ÌìŒÓ耔ÄÁăŒțÊ꣩”Ă”œ![]() Ààč€ÈËÉúČúÄÜÁŠ”ÄŸ„Ҷ͌ŁšŚóÍŒŁ©ŁŹ
Ààč€ÈËÉúČúÄÜÁŠ”ÄŸ„Ҷ͌ŁšŚóÍŒŁ©ŁŹ![]() Ààč€ÈËÉúČúÄÜÁŠ”ÄÆ”ÂÊ·ÖČŒÖ±·œÍŒŁšÓÒÍŒŁ©.
Ààč€ÈËÉúČúÄÜÁŠ”ÄÆ”ÂÊ·ÖČŒÖ±·œÍŒŁšÓÒÍŒŁ©.

(1)ÎÊ![]() ÀàĄą
ÀàĄą![]() Ààč€ÈËžśłéČéÁ˶àÉÙč€ÈËŁŹČąÇółöÖ±·œÍŒÖĐ”Ä
Ààč€ÈËžśłéČéÁ˶àÉÙč€ÈËŁŹČąÇółöÖ±·œÍŒÖĐ”Ä![]() Ł»
Ł»
(2)Çó![]() Ààč€ÈËÉúČúÄÜÁŠ”ÄÖĐλÊ꣏ȹčÀŒÆ
Ààč€ÈËÉúČúÄÜÁŠ”ÄÖĐλÊ꣏ȹčÀŒÆ![]() Ààč€ÈËÉúČúÄÜÁŠ”ÄÆœŸùÊęŁšÍŹÒ»ŚéÖĐ”ÄÊęŸĘÓÞÌéÇűŒä”ÄÖĐ”ăÖ”ŚśŽú±íŁ©Ł»
Ààč€ÈËÉúČúÄÜÁŠ”ÄÆœŸùÊęŁšÍŹÒ»ŚéÖĐ”ÄÊęŸĘÓÞÌéÇűŒä”ÄÖĐ”ăÖ”ŚśŽú±íŁ©Ł»
(3)Èôč涚ÉúČúÄÜÁŠÔÚ![]() ÄÚÎȘÄÜÁŠÓĆĐ㣏ÓÉÒÔÉÏÍłŒÆÊęŸĘÔÚŽđÌâżšÉÏÍêłÉÏÂĂæ”Ä
ÄÚÎȘÄÜÁŠÓĆĐ㣏ÓÉÒÔÉÏÍłŒÆÊęŸĘÔÚŽđÌâżšÉÏÍêłÉÏÂĂæ”Ä![]() ÁĐÁȘ±íŁŹČąĆжÏÊÇ·ńżÉÒÔÔÚ·žŽíÎóžĆÂÊČ»łŹčę0.1%”ÄÇ°ÌáÏÂŁŹÈÏÎȘÉúČúÄÜÁŠÓëĆàŃ”Ê±Œäł€¶ÌÓĐčŰ.ÄÜÁŠÓëĆàŃ”Ê±ŒäÁĐÁȘ±í
ÁĐÁȘ±íŁŹČąĆжÏÊÇ·ńżÉÒÔÔÚ·žŽíÎóžĆÂÊČ»łŹčę0.1%”ÄÇ°ÌáÏÂŁŹÈÏÎȘÉúČúÄÜÁŠÓëĆàŃ”Ê±Œäł€¶ÌÓĐčŰ.ÄÜÁŠÓëĆàŃ”Ê±ŒäÁĐÁȘ±í
¶ÌÆÚĆàŃ” | ł€ÆÚĆàŃ” | șÏŒÆ | |
ÄÜÁŠÓĆĐă | |||
ÄÜÁŠČ»ÓĆĐă | |||
șÏŒÆ |
ČÎżŒÊęŸĘŁș
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
ČÎżŒč«ÊœŁș![]() ŁŹÆäÖĐ
ŁŹÆäÖĐ![]() .
.
ĄŸÌâÄżĄżșŁËźŃűÖłłĄœűĐĐij˟ČúÆ·”ÄĐÂĄąŸÉÍűÏäŃűÖł·œ·š”ÄČúÁż¶Ô±ÈŁŹÊŐ»ńʱžśËæ»úłéÈĄÁË100žöÍűÏ䣏ČâÁżžśÏäËźČúÆ·”ÄČúÁżŁš”„λŁșkgŁ©, ÆäÆ”ÂÊ·ÖČŒÖ±·œÍŒÈçÏÂŁș

Łš1Ł©ŒÇA±íÊŸÊÂŒțĄ°ŸÉŃűÖł·š”ÄÏäČúÁż”ÍÓÚ50 kgĄ±ŁŹčÀŒÆA”ÄžĆÂÊŁ»
Łš2Ł©ÌîĐŽÏÂĂæÁĐÁȘ±íŁŹČąžùŸĘÁĐÁȘ±íĆжÏÊÇ·ńÓĐ99%”Ä°ŃÎŐÈÏÎȘÏäČúÁżÓëŃűÖł·œ·šÓĐčŰŁș
ÏäČúÁżŁŒ50 kg | ÏäČúÁżĄĘ50 kg | |
ŸÉŃűÖł·š | ||
ĐÂŃűÖł·š |
Łš3Ł©žùŸĘÏäČúÁż”ÄÆ”ÂÊ·ÖČŒÖ±·œÍŒŁŹ¶ÔŐâÁœÖÖŃűÖł·œ·š”ÄÓĆÁÓœűĐĐ±ÈœÏ.
žœŁș
PŁš | 0.050 0.010 0.001 |
k | 3.841 6.635 10.828 |
![]() .
. ![]()



