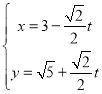题目内容
【题目】选修4-4:坐标系与参数方程
已知曲线![]() 的极坐标方程是
的极坐标方程是![]() ,以极点为原点,极轴为
,以极点为原点,极轴为![]() 轴的正半轴建立平面直角坐标系,直线
轴的正半轴建立平面直角坐标系,直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数).
为参数).
(I)写出直线![]() 的一般方程与曲线
的一般方程与曲线![]() 的直角坐标方程,并判断它们的位置关系;
的直角坐标方程,并判断它们的位置关系;
(II)将曲线![]() 向左平移
向左平移![]() 个单位长度,向上平移
个单位长度,向上平移![]() 个单位长度,得到曲线
个单位长度,得到曲线![]() ,设曲线
,设曲线![]() 经过伸缩变换
经过伸缩变换![]() 得到曲线
得到曲线![]() ,设曲线
,设曲线![]() 上任一点为
上任一点为![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)见解析;(2)![]() .
.
【解析】试题分析:(I)极坐标方程两边乘以![]() ,利用
,利用![]() 转化成直角坐标方程,然后将直线的参数方程的上式化简成
转化成直角坐标方程,然后将直线的参数方程的上式化简成![]() 代入下式消去参数
代入下式消去参数![]() 即可,最后利用圆心到直线的距离与半径比较即可判定位置关系;(II)根据伸缩变换公式求出变换后的曲线方程,然后利用参数方程表示出曲线上任意一点,代入
即可,最后利用圆心到直线的距离与半径比较即可判定位置关系;(II)根据伸缩变换公式求出变换后的曲线方程,然后利用参数方程表示出曲线上任意一点,代入![]() ,根据三角函数的辅助角公式,求出其范围即可.
,根据三角函数的辅助角公式,求出其范围即可.
试题解析:(I)直线![]() 的一般方程为
的一般方程为![]() ,
,
曲线![]() 的直角坐标方程为
的直角坐标方程为![]() .
.
因为 ,
,
所以直线![]() 和曲线
和曲线![]() 相切.
相切.
(II)曲线![]() 为
为![]() .
.
曲线![]() 经过伸缩变换
经过伸缩变换![]()
得到曲线![]() 的方程为
的方程为![]() ,
,
则点![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),
为参数),
所以![]() ,
,
所以![]() 的取值范围为
的取值范围为![]() .
.

练习册系列答案
相关题目
【题目】某出租车公司为了解本公司出租车司机对新法规的知晓情况,随机对![]() 名出租车司机进行调查,调查问卷共
名出租车司机进行调查,调查问卷共![]() 道题,答题情况如下表:
道题,答题情况如下表:
答对题目数 |
|
|
|
|
女 |
|
|
|
|
男 |
|
|
|
|
(I)如果出租车司机答对题目大于等于![]() ,就认为该司机对新法规的知晓情况比较好,试估计该公司的出租车司机对新法规知晓情况比较好的概率;
,就认为该司机对新法规的知晓情况比较好,试估计该公司的出租车司机对新法规知晓情况比较好的概率;
(II)从答对题目数小于![]() 的出租车司机中选出
的出租车司机中选出![]() 人做进一步的调查,求选出的
人做进一步的调查,求选出的![]() 人中至少有一名女出租车司机的概率.
人中至少有一名女出租车司机的概率.