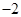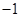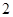题目内容
设△ABC的三个内角为A,B,C,向量m=( sinA,sinB),
sinA,sinB),
n=(cosB, cosA),若m·n=1+cos(A+B),则C=( )
cosA),若m·n=1+cos(A+B),则C=( )
(A) (B)
(B) (C)
(C) (D)
(D)
 sinA,sinB),
sinA,sinB),n=(cosB,
 cosA),若m·n=1+cos(A+B),则C=( )
cosA),若m·n=1+cos(A+B),则C=( )(A)
 (B)
(B) (C)
(C) (D)
(D)
C
依题意得 sinAcosB+
sinAcosB+ cosAsinB
cosAsinB
=1+cos(A+B), sin(A+B)=1+cos(A+B),
sin(A+B)=1+cos(A+B),
 sinC+cosC=1,2sin(C+
sinC+cosC=1,2sin(C+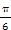 )=1,sin(C+
)=1,sin(C+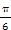 )=
)= .
.
又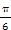 <C+
<C+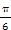 <
<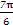 ,
,
因此C+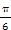 =
= ,C=
,C= ,选C.
,选C.
 sinAcosB+
sinAcosB+ cosAsinB
cosAsinB=1+cos(A+B),
 sin(A+B)=1+cos(A+B),
sin(A+B)=1+cos(A+B), sinC+cosC=1,2sin(C+
sinC+cosC=1,2sin(C+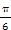 )=1,sin(C+
)=1,sin(C+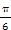 )=
)= .
.又
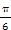 <C+
<C+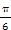 <
<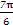 ,
,因此C+
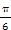 =
= ,C=
,C= ,选C.
,选C.
练习册系列答案
相关题目
 ,
,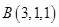 ,
,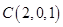 .
.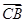 与
与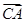 的夹角;
的夹角; =(x,2x),
=(x,2x), =(-3x,2),且
=(-3x,2),且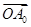 +
+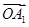 +…+OAn-1+
+…+OAn-1+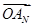 |等于( )
|等于( ) b=(3,1),c=(x,3),若(2a+b)∥c,则x= .
b=(3,1),c=(x,3),若(2a+b)∥c,则x= .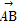 =a,
=a,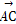 =b,对于平面ABC上任意一点O,动点P满足
=b,对于平面ABC上任意一点O,动点P满足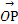 =
=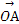 +λa+λb,则动点P的轨迹所过的定点为 .
+λa+λb,则动点P的轨迹所过的定点为 .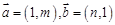 ,若
,若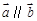 ,则
,则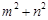 的最小值为 .
的最小值为 .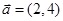 与向量
与向量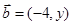 垂直,则
垂直,则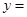 ( )
( )