题目内容
若非零向量
,
满足|
-
|=|
|,则( )
| a |
| b |
| a |
| b |
| b |
A.|2
| B.|2
| C.|2
| D.|2
|
若两向量共线,则由于a,b是非零向量,且|a-b|=|b|,
∴必有a=2b;代入可知只有A、C满足;
若两向量不共线,注意到向量模的几何意义,
∴可以构造如图所示的三角形,使其满足OB=AB=BC;
令
=a,
=b,则
=a-b,
∴
=a-2b且|a-b|=|b|;又BA+BC>AC
∴|a-b|+|b|>|a-2b|
∴|2b|>|a-2b|
故选A.

∴必有a=2b;代入可知只有A、C满足;
若两向量不共线,注意到向量模的几何意义,
∴可以构造如图所示的三角形,使其满足OB=AB=BC;
令
| OA |
| OB |
| BA |
∴
| CA |
∴|a-b|+|b|>|a-2b|
∴|2b|>|a-2b|
故选A.


练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目

 sinA,sinB),
sinA,sinB), (B)
(B) (C)
(C) (D)
(D)
 与
与 均为单位向量,它们的夹角为
均为单位向量,它们的夹角为 ,那么
,那么 等于( )
等于( )


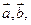 “
“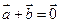 ”是“
”是“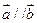 ”的( )
”的( ) , 若a//b, 则实数m等于
, 若a//b, 则实数m等于
