题目内容

3．若方程ax-x-a=0有两个实数解，则a的取值范围是（　　）
A．（0，+∞）B．（1，+∞）C．（0，1）D．（0，2）

分析 方程ax-x-a=0变形为：方程ax=x+a，由题意得，函数y=ax与函数y=a+x 有两个不同的交点，结合图象得出结论．

解答 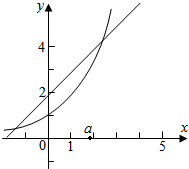解：方程ax-x-a=0变形为：方程ax=x+a，
由题意得，方程ax-x-a=0有两个不同的实数解，
即函数y=ax与函数y=a+x 有两个不同的交点，
y=ax的图象过定点（0，1），直线y=x+a 的图象过定点（0，a），
如图所示：
故直线y=x+a在y轴上的截距a大于1时，
函数y=ax与函数y=a+x 有两个不同的交点．
故选B．

点评 本题考查方程根的个数的判断，解答关键是灵活运用数形结合及转化的数学思想．

练习册系列答案
相关题目
13．已知正方体的外接球的体积是$\frac{4π}{3}$，则这个正方体的棱长是$\frac{{2\sqrt{3}}}{3}$．
14．若A${\;}_{n}^{2}$=4C${\;}_{n-1}^{2}$，则n的值为（　　）
A．7B．6C．5D．4
11．设椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左、右焦点分别为F1，F2，离心率为$\frac{1}{2}$，过上顶点A与AF2垂直的直线交x轴于Q点，且2$\overrightarrow{{F}_{1}{F}_{2}}$+$\overrightarrow{{F}_{2}Q}$=$\overrightarrow{0}$，过A，Q，F2三点的圆恰好与直线x-$\sqrt{3}$y-3=0相切．
（Ⅰ）求椭圆C的方程；
（Ⅱ）过F2的直线l与椭圆C交于不同的两点M，N，△F1MN的面积是否存在最大值？若存在，求出这个最大值及此事直线l的方程，若不存在，请说明理由．
18．如图，某乡镇计划以公路MN为对角线修建一个矩形的农业观光园区AMPN，在观光园区内再建造一矩形服务中心ABCD，已知B在AM上，C在MN上，D在AN上，公路MN的长度为10千米，设∠AMN=θ．
（1）当θ为多少时，农业观光园区AMPN的面积最大；
（2）若θ=30°，则CM的长度为多少时，服务中心ABCD的面积最大．
8．当x∈（1，2]时，不等式x2+mx+4＞0恒成立，则m的取值范围是m＞-4．
15．在空间直角坐标系中，点P（-2，1，3）关于坐标平面xOy对称的点的坐标为（-2，1，-3）．
4．设函数f（x）=cos2（$\frac{π}{2}+x$）+$\sqrt{3}$sin（$\frac{π}{2}$+x）cos（$\frac{5π}{2}$-x），x∈R．
（1）求函数f（x）的单调递增区间，并求f（x）在区间[-$\frac{π}{4}$，$\frac{π}{6}$]上的最小值；
（2）在三角形ABC中，a，b，c分别是角A，B，C的对边，A为锐角，若f（A）+f（-A）=$\frac{3}{2}$，b+c=7，三角形ABC的面积为2$\sqrt{3}$，求a．
5．若命题p：x2+2x+a=0有实根，命题q：函数f（x）=（a2-a）x是增函数，若p∨q为真，p∧q为假，则a的取值范围是（　　）
A．a＞0B．a≥0C．a＞1D．a≥1

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网