题目内容
8.当x∈(1,2]时,不等式x2+mx+4>0恒成立,则m的取值范围是m>-4.分析 ①构造函数:f(x)=x2+mx+4,x∈(1,2].②讨论对称轴x=-$\frac{m}{2}$f(x)的单调性,③讨论判别式的符号,从而求出m的范围.
解答 解:根据题意,构造函数:f(x)=x2+mx+4,x∈(1,2].
由于当x∈(1,2]时,不等式x2+mx+4>0恒成立.
①△<0即m2-16<0时,不等式x2+mx+4>0恒成立,解得:-4<m<4,
②△=0即m2-16=0,m=±4时,显然m=-4不合题意,m=4符合题意,
③△>0时,只需$\left\{\begin{array}{l}{△{=m}^{2}-16>0}\\{-\frac{m}{2}<1}\\{f(1)=1+m+4≥0}\end{array}\right.$或$\left\{\begin{array}{l}{△{=m}^{2}-16>0}\\{-\frac{m}{2}>2}\\{f(2)=4+2m+4>0}\end{array}\right.$,解得:m>4,
综上:m>-4,
故答案为:m>-4.
点评 本题考查二次函数图象讨论以及单调性问题,是一道中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
18.执行下面的程序框图,如果输入的N=4,那么输出的S=( )
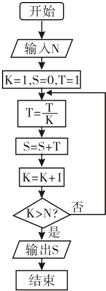

| A. | 1+$\frac{1}{2}+\frac{1}{3}+\frac{1}{4}$ | B. | 1+$\frac{1}{2}$+$\frac{1}{3×2}$+$\frac{1}{4×3×2}$ | ||
| C. | 1+$\frac{1}{2}+\frac{1}{3}+\frac{1}{4}$+$\frac{1}{5}$ | D. | 1+$\frac{1}{2}$+$\frac{1}{3×2}$+$\frac{1}{4×3×2}$+ |
16.已知a、b表示不同的直线,α表示平面,其中正确的命题有( )
①若a∥α,b∥α,则a∥b;②若a∥b,b∥α,则a∥α;③若a⊥α,b⊥α,则a∥b;④若a、b与α所成的角相等,则a∥b.
①若a∥α,b∥α,则a∥b;②若a∥b,b∥α,则a∥α;③若a⊥α,b⊥α,则a∥b;④若a、b与α所成的角相等,则a∥b.
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 4个 |
3.若方程ax-x-a=0有两个实数解,则a的取值范围是( )
| A. | (0,+∞) | B. | (1,+∞) | C. | (0,1) | D. | (0,2) |
13.在平行四边形ABCD中,点E是BC的中点,$\overrightarrow{BA}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,则$\overrightarrow{DE}$=( )
| A. | $\overrightarrow{a}-\frac{1}{2}\overrightarrow{b}$ | B. | $\overrightarrow{a}+\frac{1}{2}\overrightarrow{b}$ | C. | -$\overrightarrow{a}-\frac{1}{2}\overrightarrow{b}$ | D. | -$\overrightarrow{a}+\frac{1}{2}\overrightarrow{b}$ |
20.对两个变量y和x进行回归分析,得到一组样本数据:(x1,y1),(x2,y2),…,(xn,yn),则下列说法不正确的是( )
| A. | 若求得的回归方程为$\widehat{y}$=0.9x-0.3,则变量y和x之间具有正的相关关系 | |
| B. | 样本数据得到的回归直线必过样本点的中心($\overline{x}$,$\overline{y}$) | |
| C. | 残差平方和$\sum_{i=1}^{n}$(yi-$\widehat{y}$i)2越小,说明拟合的效果越好 | |
| D. | 用相关指数R2=1-$\frac{\sum_{i=1}^{n}({y}_{i}-\widehat{{y}_{i}})^{2}}{\sum_{i=1}^{n}({y}_{i}-\overline{y})^{2}}$刻画回归效果,R2的值越小,说明拟合的效果越好 |
10.已知an=$\frac{n+10}{2n+1}$,Tn是数列{an}的前n项积,当Tn取到最大值时,n的值为( )
| A. | 9 | B. | 8 | C. | 8或9 | D. | 9或10 |
