题目内容
已知奇函数f(x)是定义在(-3,3)上的减函数,且满足不等式f(x-3)+f(x2-3)<0,设不等式解集为A,B=A∪{x|1≤x≤ },求函数g(x)=-3x2+3x-4(x∈B)的最大值。
},求函数g(x)=-3x2+3x-4(x∈B)的最大值。
 },求函数g(x)=-3x2+3x-4(x∈B)的最大值。
},求函数g(x)=-3x2+3x-4(x∈B)的最大值。-4
由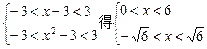 且x≠0,故0<x<
且x≠0,故0<x<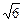 ,
,
又∵f(x)是奇函数,∴f(x-3)<-f(x2-3)=f(3-x2),
又f(x)在(-3,3)上是减函数,
∴x-3>3-x2,即x2+x-6>0,解得x>2或x<-3,
综上得2<x<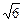 ,即A={x|2<x<
,即A={x|2<x<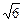 },
},
∴B=A∪{x|1≤x≤ }={x|1≤x<
}={x|1≤x<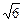 },
},
又g(x)=-3x2+3x-4=-3(x-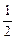 )2-
)2-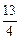 知g(x)在B上为减函数,
知g(x)在B上为减函数,
∴g(x)max=g(1)=-4。
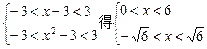 且x≠0,故0<x<
且x≠0,故0<x<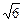 ,
,又∵f(x)是奇函数,∴f(x-3)<-f(x2-3)=f(3-x2),
又f(x)在(-3,3)上是减函数,
∴x-3>3-x2,即x2+x-6>0,解得x>2或x<-3,
综上得2<x<
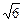 ,即A={x|2<x<
,即A={x|2<x<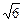 },
},∴B=A∪{x|1≤x≤
 }={x|1≤x<
}={x|1≤x<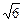 },
},又g(x)=-3x2+3x-4=-3(x-
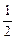 )2-
)2-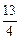 知g(x)在B上为减函数,
知g(x)在B上为减函数,∴g(x)max=g(1)=-4。

练习册系列答案
相关题目
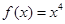 ;(2)
;(2)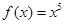 ,(3)
,(3)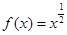 ,(4)
,(4)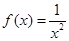 中是奇函数的有( )
中是奇函数的有( )





 恰有一个零点,求
恰有一个零点,求 的值
的值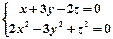 ,则方程组的解(x,y,z)= 。
,则方程组的解(x,y,z)= 。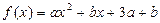 是定义域为
是定义域为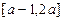 的偶函数,则
的偶函数,则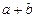 的值是( )
的值是( )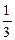 ;
;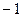
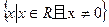 又f(x)在
又f(x)在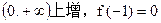 ,则f(x)>0的解集是( )
,则f(x)>0的解集是( )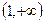 B (0,1) C
B (0,1) C 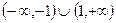 D
D 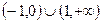
 为偶函数,则
为偶函数,则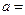 .
.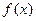 是
是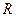 上的奇函数,且当
上的奇函数,且当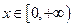 时,
时,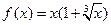 ,则当
,则当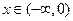 时
时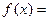 _____________________。
_____________________。