题目内容
设抛物线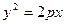 (
(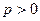 )上个点到直线3x+4y+12= 0的距离的最小值为1,求p的值。
)上个点到直线3x+4y+12= 0的距离的最小值为1,求p的值。
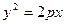 (
(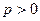 )上个点到直线3x+4y+12= 0的距离的最小值为1,求p的值。
)上个点到直线3x+4y+12= 0的距离的最小值为1,求p的值。p=

解法1:设M( ,
, )为抛物线
)为抛物线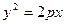 (
(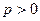 )上任意一点,则M到直线3x+4y+12= 0的距离为d=
)上任意一点,则M到直线3x+4y+12= 0的距离为d= =
=
 。
。
因为 =1,所以8p-
=1,所以8p-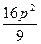 >0,即0<p<
>0,即0<p< 且
且 (8p-
(8p-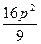 )=1,
)=1,
所以p= 。
。
解法2:由题意可知,抛物线必在直线3x+4y+12= 0的上方。则直线3x+4y+12= 0上方且和它相距为1的直线方程为3x+4y+7= 0。
由题意知 只有一解。消去x得:
只有一解。消去x得: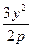 +4y+7= 0。
+4y+7= 0。
由△= 16-4× ×7=0,所以p=
×7=0,所以p= 。
。
 ,
, )为抛物线
)为抛物线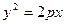 (
(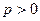 )上任意一点,则M到直线3x+4y+12= 0的距离为d=
)上任意一点,则M到直线3x+4y+12= 0的距离为d= =
=
 。
。因为
 =1,所以8p-
=1,所以8p-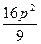 >0,即0<p<
>0,即0<p< 且
且 (8p-
(8p-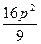 )=1,
)=1,所以p=
 。
。解法2:由题意可知,抛物线必在直线3x+4y+12= 0的上方。则直线3x+4y+12= 0上方且和它相距为1的直线方程为3x+4y+7= 0。
由题意知
 只有一解。消去x得:
只有一解。消去x得: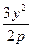 +4y+7= 0。
+4y+7= 0。由△= 16-4×
 ×7=0,所以p=
×7=0,所以p= 。
。
练习册系列答案
相关题目
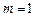 时,求椭圆的标准方程及其右准线的方程;
时,求椭圆的标准方程及其右准线的方程;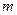 表示P点的坐标;
表示P点的坐标;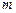 ,使得
,使得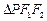 的边长是连续的自然数,若存在,求出这样的实数
的边长是连续的自然数,若存在,求出这样的实数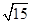 ,求抛物线的标准方程.
,求抛物线的标准方程.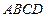 的两顶点
的两顶点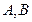 在抛物线
在抛物线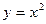 上,
上,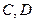 两点在直线
两点在直线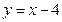 上,求正方形的边长
上,求正方形的边长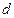 。
。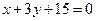 上抛物线的标准方程.
上抛物线的标准方程.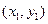 ,C
,C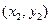 都在抛物线
都在抛物线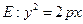 上,△ABC的重心与此抛物线E的焦点F重合. (1)写出抛物线E的方程及焦点坐标; (2)求线段BC的中点M的坐标及BC边所在的直线方程.
上,△ABC的重心与此抛物线E的焦点F重合. (1)写出抛物线E的方程及焦点坐标; (2)求线段BC的中点M的坐标及BC边所在的直线方程.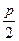 ),则点M的横坐标是( )
),则点M的横坐标是( )