题目内容
已知抛物线顶点在原点,焦点在坐标轴上,又知此抛物线上的一点A(m,-3)到焦点F的距离为5,求m的值,并写出此抛物线的方程.
y2=2x,m= ;y2=-2x,m=-
;y2=-2x,m=- ;y2=18x,m=
;y2=18x,m= ;y2=-18x,m=-
;y2=-18x,m=-
 ;y2=-2x,m=-
;y2=-2x,m=- ;y2=18x,m=
;y2=18x,m= ;y2=-18x,m=-
;y2=-18x,m=-
①若抛物线开口方向向下,设抛物线方程为x2=-2py(p>0),
这时准线方程为y=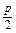 ,
,
由抛物线定义知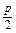 -(-3)=5,解得p=4,
-(-3)=5,解得p=4,
∴抛物线方程为x2=-8y,
这时将点A(m,-3)代入方程,得m=±2 .
.
②若抛物线开口方向向左或向右,可设抛物线方程为y2="2ax" (a≠0),从p=|a|知准线方程可统一成x=- 的形式,于是从题设有
的形式,于是从题设有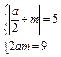 ,
,
解此方程组可得四组解
 ,
, ,
, ,
, .
.
∴y2=2x,m= ;y2=-2x,m=-
;y2=-2x,m=- ;y2=18x,m=
;y2=18x,m= ;y2=-18x,m=-
;y2=-18x,m=- .
.
这时准线方程为y=
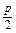 ,
,由抛物线定义知
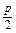 -(-3)=5,解得p=4,
-(-3)=5,解得p=4,∴抛物线方程为x2=-8y,
这时将点A(m,-3)代入方程,得m=±2
 .
.②若抛物线开口方向向左或向右,可设抛物线方程为y2="2ax" (a≠0),从p=|a|知准线方程可统一成x=-
 的形式,于是从题设有
的形式,于是从题设有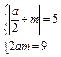 ,
,解此方程组可得四组解
 ,
, ,
, ,
, .
.∴y2=2x,m=
 ;y2=-2x,m=-
;y2=-2x,m=- ;y2=18x,m=
;y2=18x,m= ;y2=-18x,m=-
;y2=-18x,m=- .
.
练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
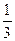 x2上的两点A与B的横坐标恰好是关于x的方程x2+px+q=0(p、q∈R,p、q是常数)的两个实根,则直线AB的方程是_____________.
x2上的两点A与B的横坐标恰好是关于x的方程x2+px+q=0(p、q∈R,p、q是常数)的两个实根,则直线AB的方程是_____________.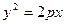 (
(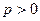 )上个点到直线3x+4y+12= 0的距离的最小值为1,求p的值。
)上个点到直线3x+4y+12= 0的距离的最小值为1,求p的值。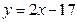 上,另外两个顶点在抛物线
上,另外两个顶点在抛物线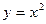 上.则该正方形面积的最小值为 .
上.则该正方形面积的最小值为 .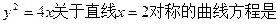 ( )
( )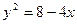 B
B 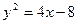 C
C 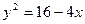 D
D 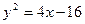
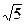 .
.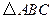 的顶点
的顶点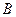 ,
,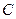 的坐标分别为
的坐标分别为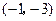 ,
, ,若点
,若点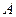 在抛物线
在抛物线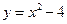 上移动,求
上移动,求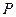 的轨迹.
的轨迹. 一光源在点M(
一光源在点M( ,4)处,由其发出的光线沿平行于抛物线的轴的方向射向抛物线上的点P,折射后又射向抛物线上的点Q,再折射后,又沿平行于抛物线的轴的方向射出,途中遇到直线l: 2x-4y-17=0上的点N,再折射后又射回点M(如下图所示)
,4)处,由其发出的光线沿平行于抛物线的轴的方向射向抛物线上的点P,折射后又射向抛物线上的点Q,再折射后,又沿平行于抛物线的轴的方向射出,途中遇到直线l: 2x-4y-17=0上的点N,再折射后又射回点M(如下图所示)