题目内容
(本小题满分14分)
已知椭圆C: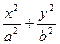 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为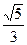 ,短轴一个端点到右焦点的距离为3.
,短轴一个端点到右焦点的距离为3.
(1)求椭圆C的方程;
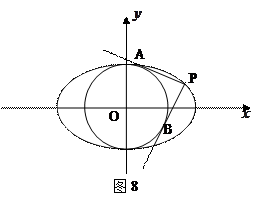
(2)过椭圆C上的动点P引圆O: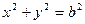 的两条切线PA、PB,A、B分别为切点,试探究椭圆C上是否存在点P,由点P向圆O所引的两条切线互相垂直?若存在,请求出点P的坐标;若不存在,请说明理由.
的两条切线PA、PB,A、B分别为切点,试探究椭圆C上是否存在点P,由点P向圆O所引的两条切线互相垂直?若存在,请求出点P的坐标;若不存在,请说明理由.
已知椭圆C:
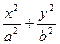 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为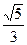 ,短轴一个端点到右焦点的距离为3.
,短轴一个端点到右焦点的距离为3.
(1)求椭圆C的方程;
(2)过椭圆C上的动点P引圆O:
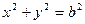 的两条切线PA、PB,A、B分别为切点,试探究椭圆C上是否存在点P,由点P向圆O所引的两条切线互相垂直?若存在,请求出点P的坐标;若不存在,请说明理由.
的两条切线PA、PB,A、B分别为切点,试探究椭圆C上是否存在点P,由点P向圆O所引的两条切线互相垂直?若存在,请求出点P的坐标;若不存在,请说明理由.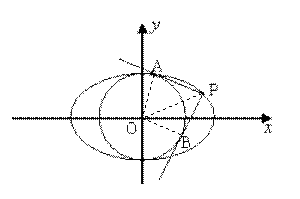 解:(1)设椭圆的半焦距为
解:(1)设椭圆的半焦距为 ,依题意
,依题意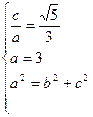 ……3分
……3分 ,……4分
,……4分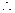 所求椭圆方程为
所求椭圆方程为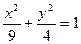 .……5分
.……5分(2)如图,设P点坐标为
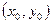 ,……6分
,……6分若
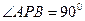 ,则有
,则有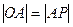 .……7分
.……7分即
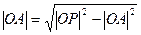 ……8分
……8分有
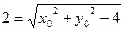
两边平方得
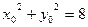 ……①……9分
……①……9分又因为
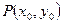 在椭圆上,所以
在椭圆上,所以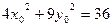 ……②……10分
……②……10分①,②联立解得
 ……11分
……11分所以满足条件的有以下四组解
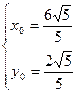 ,
,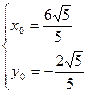 ,
,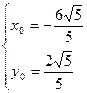 ,
,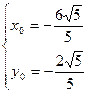 ……13分
……13分所以,椭圆C上存在四个点
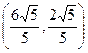 ,
, ,
, ,
,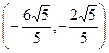 ,分别由这四个点向圆O所引的两条切线均互相垂直. ……14分
,分别由这四个点向圆O所引的两条切线均互相垂直. ……14分略

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
 的左顶点、右焦点分别为A、F,点B(0,b),若
的左顶点、右焦点分别为A、F,点B(0,b),若 ,则该双曲线离心率e的值为( )
,则该双曲线离心率e的值为( ) B.
B. C.
C. D.
D.
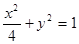 共焦点且过点
共焦点且过点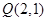 的双曲线方程是
的双曲线方程是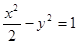
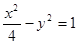

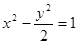
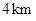 的
的 ,
, 两点,要围垦出以
两点,要围垦出以 为一条对角线的平行四边形区域建制造厂。按照规划,围墙总长为
为一条对角线的平行四边形区域建制造厂。按照规划,围墙总长为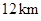 .在设计图纸上,建立平面直角坐标系如图(
.在设计图纸上,建立平面直角坐标系如图( 为
为 ,
, 的坐标满足的方程是
的坐标满足的方程是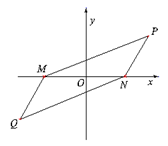

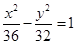

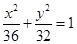
 与直线
与直线 +3有两个不同的公共点,则实数 k 的取值范围是( )
+3有两个不同的公共点,则实数 k 的取值范围是( )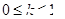
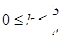
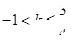
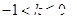
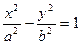 (
(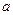 >0,
>0,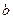 >0)的左、右焦点为
>0)的左、右焦点为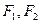 ,设
,设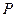 是双曲线右支上一点,
是双曲线右支上一点,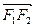 在
在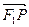 上的投影的大小恰为
上的投影的大小恰为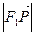 ,且它们的夹角为
,且它们的夹角为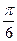 ,则双曲线的离心率
,则双曲线的离心率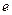 为( )
为( )



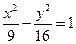 ,
,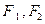 分别为它的
分别为它的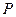 为双曲线上一点,设
为双曲线上一点,设 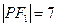 ,
,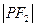 的值为 ▲ .
的值为 ▲ . 的焦点为焦点,离心率为2的双曲线方程为 。
的焦点为焦点,离心率为2的双曲线方程为 。