题目内容
：已知双曲线
的左顶点、右焦点分别为A、F，点B（0，b），若
，则该双曲线离心率e的值为（ ）
A．
B．
C．
D．
的左顶点、右焦点分别为A、F，点B（0，b），若，则该双曲线离心率e的值为（ ）A．
B． C． D．：B
：
分析：通过，判断三角形ABF的关系，利用三角形的关系，得到a，b，c的关系，结合双曲线a，b，c关系求出双曲线的离心率即可．
解：因为双曲线的左顶点、右焦点分别为A、F，点B（0，b），，所以AB⊥BF，三角形ABF是直角三角形，
所以|AB|2+|BF|2=|AF|2．
即：c2+b2+c2=（a+c）2．
∵b2=c2-a2．
∴3c2-a2=（a+c）2．
∴c2-a2-ac=0，
e2-e-1=0，
解得：e=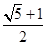
．e=
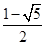（舍去）．
故答案为：B．
分析：通过
，判断三角形ABF的关系，利用三角形的关系，得到a，b，c的关系，结合双曲线a，b，c关系求出双曲线的离心率即可．解：因为双曲线
的左顶点、右焦点分别为A、F，点B（0，b），，所以AB⊥BF，三角形ABF是直角三角形，所以|AB|2+|BF|2=|AF|2．
即：c2+b2+c2=（a+c）2．
∵b2=c2-a2．
∴3c2-a2=（a+c）2．
∴c2-a2-ac=0，
e2-e-1=0，
解得：e=
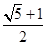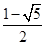．e=（舍去）．故答案为：B．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
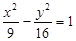有共同的渐近线,且经过点
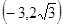的双曲线的方程为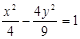 
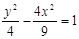
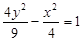
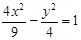
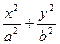=1(a＞b＞0)的离心率为
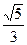,短轴一个端点到右焦点的距离为3.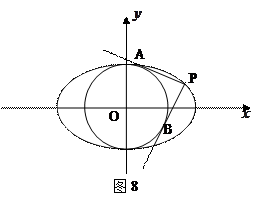
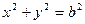的两条切线PA、PB，A、B分别为切点，试探究椭圆C上是否存在点P，由点P向圆O所引的两条切线互相垂直？若存在，请求出点P的坐标；若不存在，请说明理由.
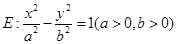的离心率为e，左、右两焦点分别为F1、F2，焦距为
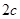，抛物线C以F2为顶点，F1为焦点,点P为抛物线与双曲线右支上的一个交点，若a|PF2|＋c|PF1|＝8a2，则e的值为 ( )
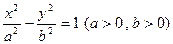的左、右焦点分别为
，
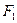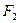，点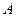
在双曲线上，且
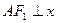轴，若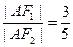
，则双曲线的离心率等于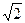 
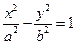(a>0,b>0)的
一个焦点作一条渐近线的垂线，垂足恰好落在曲线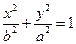
上，则双曲线的离心率为 。 高#考#资#源#
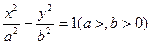与圆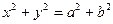
在第一象限的交点F1，F2分别是双曲线的左．右焦点，且
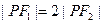，则双曲线的离心率为（ ）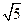
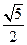
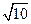
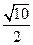
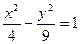的渐近线方程是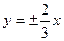 
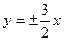
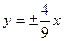
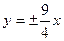
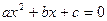无实根,则双曲线
的离心率的取值范围为.