题目内容
【题目】对于曲线C所在平面上的定点![]() ,若存在以点
,若存在以点![]() 为顶点的角
为顶点的角![]() ,使得
,使得![]() 对于曲线C上的任意两个不同的点A,B恒成立,则称角
对于曲线C上的任意两个不同的点A,B恒成立,则称角![]() 为曲线C相对于点
为曲线C相对于点![]() 的“界角”,并称其中最小的“界角”为曲线C相对于点
的“界角”,并称其中最小的“界角”为曲线C相对于点![]() 的“确界角”.曲线
的“确界角”.曲线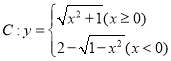 相对于坐标原点
相对于坐标原点![]() 的“确界角”的大小是 _________.
的“确界角”的大小是 _________.
【答案】![]()
【解析】
画出函数![]() 的图象,过点
的图象,过点![]() 作出两条直线与曲线无限接近,当
作出两条直线与曲线无限接近,当![]() 时,曲线
时,曲线![]() 与直线
与直线![]() 无限接近,求出
无限接近,求出![]() ,当
,当![]() 时,曲线可化为
时,曲线可化为![]() ,圆心到直线的距离为1,求得
,圆心到直线的距离为1,求得![]() ,再由两直线的夹角公式,即可求解.
,再由两直线的夹角公式,即可求解.
由题意,画出函数![]() 的图象,过点
的图象,过点![]() 作出两条直线与曲线无限接近,
作出两条直线与曲线无限接近,
设它们的方程方程为![]() ,
,![]() ,
,
当![]() 时,曲线
时,曲线![]() 与直线
与直线![]() 无限接近,即为双曲线的渐近线,可得
无限接近,即为双曲线的渐近线,可得![]() ;
;
当![]() 时,曲线可化为
时,曲线可化为![]() ,圆心到直线的距离为
,圆心到直线的距离为![]() ,
,
解得![]() ,
,
由两直线的夹角公式,可得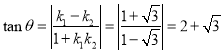 ,
,
所以曲线![]() 相对于点
相对于点![]() 的“确界角”为
的“确界角”为![]() .
.
故答案为:![]() .
.
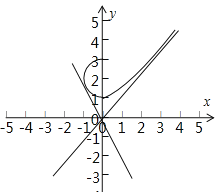

练习册系列答案
相关题目