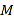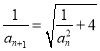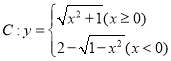Question

【题目】如图1，在平行四边形中，，，点是的中点，点是的中点，分别沿．将和折起，使得平面平面（点在平面的同侧），连接，如图2所示．

（1）求证：；

（2）当，且平面平面时，求三棱锥的体积．

Answer 1

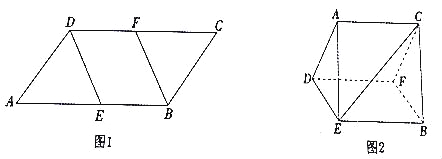
【答案】（1）见解析；（2）1

【解析】

（1）由已知可得△CBF为等边三角形，连接EF，由已知可得△BEF为等边三角形．取BF的中点O，连接OC，OE，可得CO⊥BF，EO⊥BF．从而得到BF⊥平面COE，则BF⊥CE；

（2）由（1）知，CO⊥BF，结合条件可证OE⊥BF，求得，利用锥体体积公式求解即可.

（1）∵四边形为平行四边形，，点是的中点，

∴，又，∴为等边三角形，

连接，由，，得为等边三角形．

取的中点，连接，则．

∴平面，则；

（2）由（1）知，，又平面平面，

则平面，又，

∵，

∴．

∴三棱锥的体积．