题目内容
椭圆
 的离心率为
的离心率为 ,其左焦点到点
,其左焦点到点 的距离为
的距离为 .
.
(1) 求椭圆 的标准方程;
的标准方程;
(2) 若直线 与椭圆
与椭圆 相交于
相交于 两点(
两点( 不是左右顶点),且以
不是左右顶点),且以 为直径的圆过椭圆
为直径的圆过椭圆 的右顶点,求证:直线
的右顶点,求证:直线 过定点,并求出该定点的坐标.
过定点,并求出该定点的坐标.


 的离心率为
的离心率为 ,其左焦点到点
,其左焦点到点 的距离为
的距离为 .
.(1) 求椭圆
 的标准方程;
的标准方程;(2) 若直线
 与椭圆
与椭圆 相交于
相交于 两点(
两点( 不是左右顶点),且以
不是左右顶点),且以 为直径的圆过椭圆
为直径的圆过椭圆 的右顶点,求证:直线
的右顶点,求证:直线 过定点,并求出该定点的坐标.
过定点,并求出该定点的坐标.
(1) ;(2)证明详见解析,
;(2)证明详见解析, .
.
 ;(2)证明详见解析,
;(2)证明详见解析, .
.试题分析:本题主要考查椭圆的标准方程及其几何性质、直线与椭圆相交问题等基础知识,考查学生的分析问题解决问题的能力、转化能力、计算能力.第一问,利用椭圆的离心率和左焦点到点P的距离列出方程组,解出基本量a,b,c,从而得到椭圆的标准方程;第二问,用直线与椭圆联立,消参得到关于x的方程,利用韦达定理得到
 和
和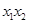 ,由于AB为直径的圆过椭圆右顶点 A2(2,0) ,所以
,由于AB为直径的圆过椭圆右顶点 A2(2,0) ,所以 ,利用向量的数量积的运算公式,将前面的式子都代入,得到
,利用向量的数量积的运算公式,将前面的式子都代入,得到 或 m = -2k,经验证都符合题意,则分别求出定点坐标,再验证,最终得到结论.
或 m = -2k,经验证都符合题意,则分别求出定点坐标,再验证,最终得到结论.试题解析:(1)由题:
 ①
①左焦点 (-c,0) 到点 P(2,1) 的距离为:
 ② 2分
② 2分由①②可解得c =" 1" , a =" 2" , b 2 = a 2-c 2 = 3. 3分
∴所求椭圆 C 的方程为
 . 4分
. 4分(2)设 A(x1,y1)、B(x2,y2),将 y =" kx" + m代入椭圆方程得
(4k 2 + 3) x 2 + 8kmx + 4m 2-12 = 0.
∴
 ,
, , 6分
, 6分且y1 = kx1 + m,y2 = kx2 + m.
∵AB为直径的圆过椭圆右顶点 A2(2,0) ,所以
 . 7分
. 7分所以 (x1-2,y1)·(x2-2,y2) = (x1-2) (x2-2) + y1y2 = (x1-2) (x2-2) + (kx1 + m) (kx2 + m)
= (k 2 + 1) x1x2 + (km-2) (x1 + x2) + m 2 + 4
= (k 2 + 1)·
 -(km-2)·
-(km-2)· + m 2 + 4 =" 0" . 10分
+ m 2 + 4 =" 0" . 10分整理得 7m 2 + 16km + 4k 2 = 0.∴
 或 m = -2k 都满足 △ > 0. 12分
或 m = -2k 都满足 △ > 0. 12分若 m = -2k 时,直线 l 为 y = kx-2k =" k" (x-2) ,恒过定点 A2(2,0),不合题意舍去; 13分
若
 时,直线 l 为
时,直线 l 为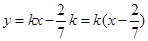 , 恒过定点
, 恒过定点 . 14分
. 14分

练习册系列答案
相关题目
 的离心率
的离心率 ,右焦点到直线
,右焦点到直线 1的距离
1的距离 ,O为坐标原点.
,O为坐标原点.
 ,则椭圆的标准方程为( ).
,则椭圆的标准方程为( ).



 ,0)和F2(
,0)和F2( ·
·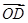 =0(O为坐标原点),求直线l的方程.
=0(O为坐标原点),求直线l的方程. 的离心率
的离心率 ,
, 分别为椭圆的长轴和短轴的端点,
分别为椭圆的长轴和短轴的端点, 为
为 中点,
中点, 为坐标原点,且
为坐标原点,且 .
. 的直线
的直线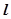 交椭圆于
交椭圆于 两点,求
两点,求 面积最大时,直线
面积最大时,直线