题目内容
设椭圆C: 的离心率
的离心率 ,右焦点到直线
,右焦点到直线 1的距离
1的距离 ,O为坐标原点.
,O为坐标原点.
(1)求椭圆C的方程;
(2)过点O作两条互相垂直的射线,与椭圆C分别交于A、B两点,证明点O到直线AB的距离为定值,并求弦AB长度的最小值.
 的离心率
的离心率 ,右焦点到直线
,右焦点到直线 1的距离
1的距离 ,O为坐标原点.
,O为坐标原点.(1)求椭圆C的方程;
(2)过点O作两条互相垂直的射线,与椭圆C分别交于A、B两点,证明点O到直线AB的距离为定值,并求弦AB长度的最小值.
(1)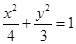 ;(2)
;(2) .
.
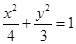 ;(2)
;(2) .
.试题分析:
解题思路:(1)利用离心率及点到直线的距离公式求解即可;(2)设出直线
 方程,联立直线与椭圆的方程,整理成关于
方程,联立直线与椭圆的方程,整理成关于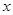 的一元二次方程,利用
的一元二次方程,利用 求解.
求解.规律总结:直线与圆锥曲线的位置关系问题,一般综合性强.一般思路是联立直线与圆锥曲线的方程,整理得关于
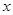 的一元二次方程,常用“设而不求”的方法进行求解.
的一元二次方程,常用“设而不求”的方法进行求解.试题解析:(1)由
 得
得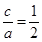 ,即
,即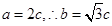
由右焦点到直线
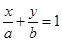 的距离为
的距离为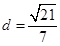
得
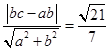 ,解得
,解得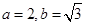 ,
,所以椭圆C的方程为
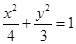 .
. (2)设A
 B
B
直线AB的方程为y=kx+m与椭圆
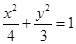 联立消去y得
联立消去y得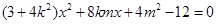

∵OA⊥OB,
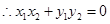
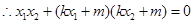
即
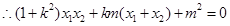
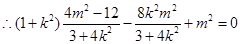
整理得

所以O到直线AB的距离

∵OA⊥OB,∴
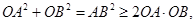
当且仅当OA=OB时取“=”
由
 得
得
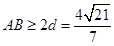 .
.即弦的长度最小值是
 .
. 
练习册系列答案
相关题目

 的离心率为
的离心率为 ,其左焦点到点
,其左焦点到点 的距离为
的距离为 .
. 的标准方程;
的标准方程; 与椭圆
与椭圆 两点(
两点( 为直径的圆过椭圆
为直径的圆过椭圆 过定点,并求出该定点的坐标.
过定点,并求出该定点的坐标.
 ,则该椭圆的标准方程为
,则该椭圆的标准方程为



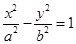
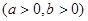 的渐近线方程为
的渐近线方程为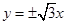 ,则以它的顶点为焦点,焦点为顶点的椭圆的离心率等于( )
,则以它的顶点为焦点,焦点为顶点的椭圆的离心率等于( )


 的离心率是
的离心率是 ,则
,则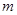 的值为 .
的值为 .