题目内容
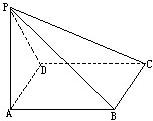
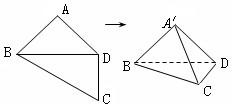
四棱锥P-ABCD的底面ABCD是边长为a的正方形,侧棱PA=a,PB=PC=
a,则它的五个面中,互相垂直的面是______.
| 2 |

∵AB=AP=a,PB=
a
∴AB2+AP2=PB2,
∴PA⊥AB
∵AD⊥AB
∴AB⊥平面PAD,
∵AB?平面ABCD,AB?平面PAB
∴面PAB⊥面PAD,面PAD⊥面ABCD,
∵CD∥AB
∴CD⊥平面PAD
∵CD?面PDC
∴面PAD⊥面PCD
故答案为面PAB⊥面PAD,面PAD⊥面ABCD,面PAD⊥面PCD
| 2 |
∴AB2+AP2=PB2,
∴PA⊥AB
∵AD⊥AB
∴AB⊥平面PAD,
∵AB?平面ABCD,AB?平面PAB
∴面PAB⊥面PAD,面PAD⊥面ABCD,
∵CD∥AB
∴CD⊥平面PAD
∵CD?面PDC
∴面PAD⊥面PCD
故答案为面PAB⊥面PAD,面PAD⊥面ABCD,面PAD⊥面PCD

练习册系列答案
相关题目
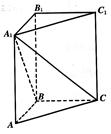
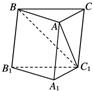
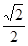 ,求点A到平面A1BC的距离.
,求点A到平面A1BC的距离.
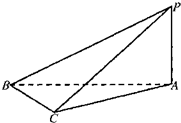
 ,对函数
,对函数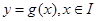 ,定义
,定义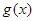 关于
关于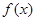 的对称函数为函数
的对称函数为函数 ,
,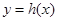 满足:对于任意
满足:对于任意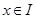 ,两个点
,两个点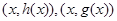 关于点
关于点 对称,若
对称,若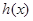 是
是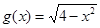 关于
关于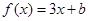 的“对称函数”,且
的“对称函数”,且 恒成立,则实数
恒成立,则实数 的取值范围是_________.
的取值范围是_________.