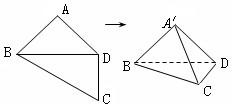
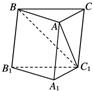
题目内容
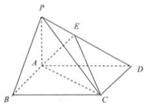
如图,在梯形ABCD中,AB∥CD,∠ADC=90°,3AD=DC=3,AB=2,E是DC上点,且满足DE=1,连接AE,将△DAE沿AE折起到△D1AE的位置,使得∠D1AB=60°,设AC与BE的交点为O.
(1)试用基向量
,
,
表示向量
;
(2)求异面直线OD1与AE所成角的余弦值;
(3)判断平面D1AE与平面ABCE是否垂直?并说明理由.

(1)试用基向量
| AB |
| AE |
| AD1 |
| OD1 |
(2)求异面直线OD1与AE所成角的余弦值;
(3)判断平面D1AE与平面ABCE是否垂直?并说明理由.

(1)∵AB∥CE,AB=CE=2,
∴四边形ABCE是平行四边形,∴O为BE的中点.
∴
=
-
=
-
(
+
)
=
-
-
.
(2)设异面直线OD1与AE所成的角为θ,
则cosθ=|cos<
,
>|=|
|,
∵
•
=(
-
-
)•
=
•
-
•
-
|
|2
=1×
×cos45°-
×2×
×cos45°-
×(
)2
=-1,
|
|=
=
,
∴cosθ=|
|=|
|=
.
故异面直线OD1与AE所成角的余弦值为
.
(3)平面D1AE⊥平面ABCE.证明如下:
取AE的中点M,则
=
-
=
∴四边形ABCE是平行四边形,∴O为BE的中点.
∴
| OD1 |
| AD1 |
| AO |
| AD1 |
| 1 |
| 2 |
| AB |
| AE |
=
| AD1 |
| 1 |
| 2 |
| AB |
| 1 |
| 2 |
| AE |
(2)设异面直线OD1与AE所成的角为θ,
则cosθ=|cos<
| OD1 |
| AE |
| ||||
|
|
∵
| OD1 |
| AE |
| AD1 |
| 1 |
| 2 |
| AB |
| 1 |
| 2 |
| AE |
| AE |
=
| AD1 |
| AE |
| 1 |
| 2 |
| AB |
| AE |
| 1 |
| 2 |
| AE |
=1×
| 2 |
| 1 |
| 2 |
| 2 |
| 1 |
| 2 |
| 2 |
=-1,
|
| OD1 |
(
|
| ||
| 2 |
∴cosθ=|
| ||||
|
|
| -1 | ||||||
|
| ||
| 3 |
故异面直线OD1与AE所成角的余弦值为
| ||
| 3 |
(3)平面D1AE⊥平面ABCE.证明如下:
取AE的中点M,则
| D1M |
| AM |
| AD1 |

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案 永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
|