题目内容
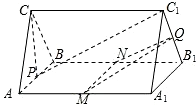
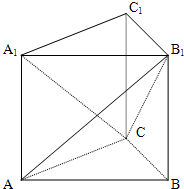
直三棱柱ABC-A1B1C1中，AC=BC=BB1=1，AB1=
（1）求证：平面AB1C⊥平面B1CB；
（2）求三棱锥A1-AB1C的体积．
| 3 |
（1）求证：平面AB1C⊥平面B1CB；
（2）求三棱锥A1-AB1C的体积．
（1）直三棱柱ABC-A1B1C1中，BB1⊥底面ABC，
则BB1⊥AB，BB1⊥BC，（3分）
又由于AC=BC=BB1=1，AB1=
，则AB=
则由AC2+BC2=AB2可知，AC⊥BC，（6分）
又由上BB1⊥底面ABC可知BB1⊥AC，则AC⊥平面B1CB，
所以有平面AB1C⊥平面B1CB；（9分）
（2）三棱锥A1-AB1C的体积VA1-AB1C=VB1-A1AC=
×
×1=
则BB1⊥AB，BB1⊥BC，（3分）
又由于AC=BC=BB1=1，AB1=
| 3 |
| 2 |
则由AC2+BC2=AB2可知，AC⊥BC，（6分）
又由上BB1⊥底面ABC可知BB1⊥AC，则AC⊥平面B1CB，
所以有平面AB1C⊥平面B1CB；（9分）
（2）三棱锥A1-AB1C的体积VA1-AB1C=VB1-A1AC=
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
练习册系列答案
相关题目
底面ABCD，PA=AD=DC=
