题目内容
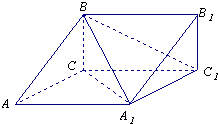
如图,直棱柱ABCD-A1B1C1D1中,底面ABCD是直角梯形,∠BAD=∠ADC=90°,AB=2AD=2CD=2.
(1)求证:AC⊥平面BB1C1C;
(2)在A1B1上是否存一点P,使得DP与平面BCB1与平面ACB1都平行?证明你的结论.
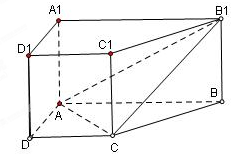
(1)求证:AC⊥平面BB1C1C;
(2)在A1B1上是否存一点P,使得DP与平面BCB1与平面ACB1都平行?证明你的结论.

证明:(1)直棱柱ABCD-A1B1C1D1中,BB1⊥平面ABCD,∴BB1⊥AC.(2分)
又∵∠BAD=∠ADC=90°,AB=2AD=2CD=2,
∴AC=
,∠CAB=45°,∴BC=
,∴BC⊥AC.(4分)
又BB1∩BC=B,BB1,BC?平面BB1C1C,∴AC⊥平面BB1C1C.(7分)
(2)存在点P,P为A1B1的中点.(8分)
证明:由P为A1B1的中点,有PB1‖AB,且PB1=
AB.(10分)
又∵DC‖AB,DC=
AB,∴DC∥PB1,且DC=PB1,
∴DCB1P为平行四边形,从而CB1∥DP.
又CB1?面ACB1,DP?面ACB1,∴DP‖面ACB1.(12分)
同理,DP‖面BCB1.(14分)
又∵∠BAD=∠ADC=90°,AB=2AD=2CD=2,
∴AC=
| 2 |
| 2 |
又BB1∩BC=B,BB1,BC?平面BB1C1C,∴AC⊥平面BB1C1C.(7分)
(2)存在点P,P为A1B1的中点.(8分)
证明:由P为A1B1的中点,有PB1‖AB,且PB1=
| 1 |
| 2 |
又∵DC‖AB,DC=
| 1 |
| 2 |
∴DCB1P为平行四边形,从而CB1∥DP.
又CB1?面ACB1,DP?面ACB1,∴DP‖面ACB1.(12分)
同理,DP‖面BCB1.(14分)

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
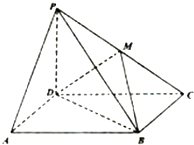
 底面ABCD,PA=AD=DC=
底面ABCD,PA=AD=DC=