题目内容
如图,已知长方体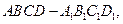
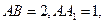
 直线
直线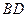 与平面
与平面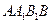 所成的角为
所成的角为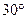 ,
, 垂直
垂直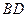 于
于
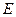 ,
,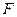 为
为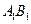 的中点.
的中点.
(1)求异面直线 与
与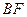 所成的角;
所成的角;
(2)求平面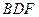 与平面
与平面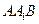 所成的二面角;
所成的二面角;
(3)求点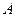 到平面
到平面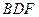 的距离.
的距离.
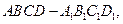
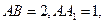
 直线
直线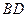 与平面
与平面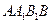 所成的角为
所成的角为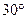 ,
, 垂直
垂直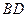 于
于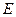 ,
,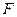 为
为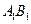 的中点.
的中点.(1)求异面直线
 与
与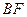 所成的角;
所成的角;(2)求平面
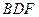 与平面
与平面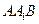 所成的二面角;
所成的二面角;(3)求点
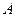 到平面
到平面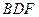 的距离.
的距离.(1)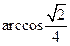 (2)
(2)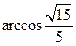 (3)
(3)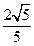
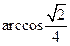 (2)
(2)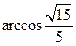 (3)
(3)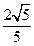
在长方体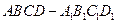 中,以
中,以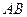 所在的直线为
所在的直线为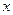 轴,以
轴,以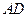 所在的直线为
所在的直线为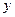 轴,
轴,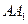 所在的直线为
所在的直线为 轴建立如图示空间直角坐标系
轴建立如图示空间直角坐标系
由已知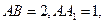 可得
可得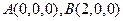 ,
,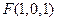
又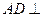 平面
平面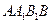 ,从而
,从而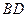 与平面
与平面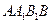 所成的角为
所成的角为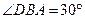 ,又
,又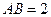 ,
,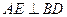 ,
,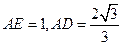 从而易得
从而易得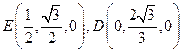
(I)因为 所以
所以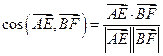 =
=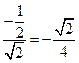
易知异面直线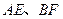 所成的角为
所成的角为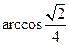 。。。。。。。。。。。。。。。。。。。。。4分
。。。。。。。。。。。。。。。。。。。。。4分
(II)易知平面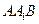 的一个法向量
的一个法向量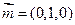 设
设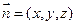 是平面
是平面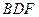 的一个法向量,
的一个法向量, 由
由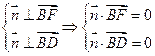
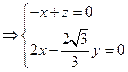
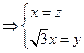
即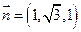 所以
所以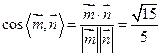 即平面
即平面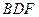 与平面
与平面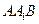 所成的二面角的大小(锐角)为
所成的二面角的大小(锐角)为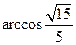
(III)点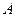 到平面
到平面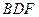 的距离,即
的距离,即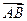 在平面
在平面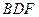 的法向量
的法向量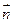 上的投影的绝对值,
上的投影的绝对值,
所以距离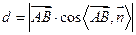 =
=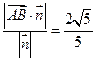 所以点
所以点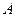 到平面
到平面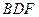 的距离为
的距离为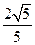
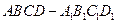 中,以
中,以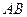 所在的直线为
所在的直线为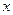 轴,以
轴,以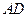 所在的直线为
所在的直线为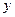 轴,
轴,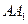 所在的直线为
所在的直线为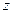 轴建立如图示空间直角坐标系
轴建立如图示空间直角坐标系由已知
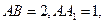 可得
可得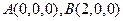 ,
,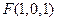
又
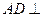 平面
平面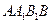 ,从而
,从而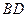 与平面
与平面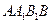 所成的角为
所成的角为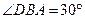 ,又
,又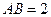 ,
,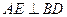 ,
,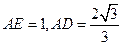 从而易得
从而易得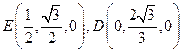
(I)因为
 所以
所以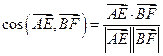 =
=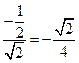
易知异面直线
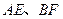 所成的角为
所成的角为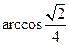 。。。。。。。。。。。。。。。。。。。。。4分
。。。。。。。。。。。。。。。。。。。。。4分(II)易知平面
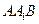 的一个法向量
的一个法向量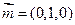 设
设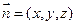 是平面
是平面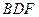 的一个法向量,
的一个法向量, 由
由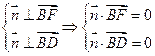
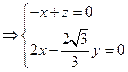
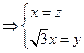
即
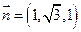 所以
所以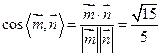 即平面
即平面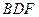 与平面
与平面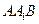 所成的二面角的大小(锐角)为
所成的二面角的大小(锐角)为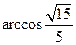
(III)点
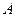 到平面
到平面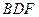 的距离,即
的距离,即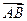 在平面
在平面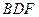 的法向量
的法向量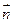 上的投影的绝对值,
上的投影的绝对值,所以距离
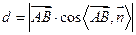 =
=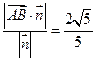 所以点
所以点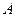 到平面
到平面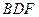 的距离为
的距离为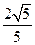

练习册系列答案
相关题目
 ,EF=EC=1,
,EF=EC=1, 
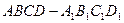 的底面ABCD是菱形,且
的底面ABCD是菱形,且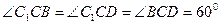 ,(1)证明:
,(1)证明: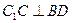 ;
;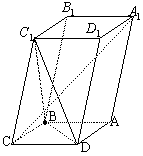
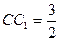 ,记面
,记面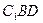 为α,面CBD为β,求二面角α -BD -β的平面角的余弦值;
为α,面CBD为β,求二面角α -BD -β的平面角的余弦值;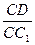 的值为多少时,能使
的值为多少时,能使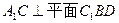 ?请给出证明.
?请给出证明. 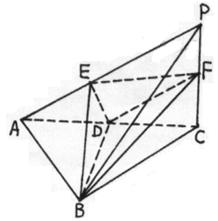
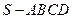 的底面是正方形,
的底面是正方形,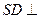 平面
平面 .
.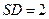 ,
,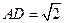 ,
,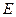 是
是 上的点.
上的点.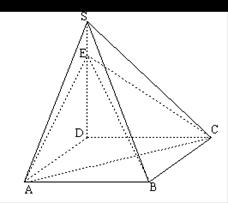
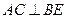 ;
;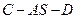 的余弦值.
的余弦值.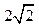 a,BC=DE=a,
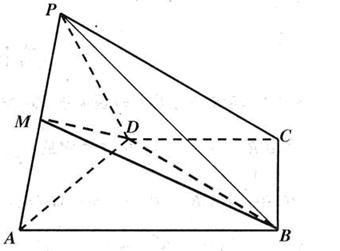
a,BC=DE=a,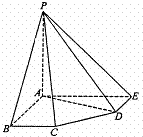 (1)求证:PA⊥平面ABCDE;
(1)求证:PA⊥平面ABCDE;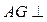 平面PDE
平面PDE ⊥平面
⊥平面 ,那么
,那么 ,平面
,平面 ,那么
,那么 平面
平面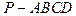 中,AD∥BC,∠ABC=90°,且
中,AD∥BC,∠ABC=90°,且 ,又PA⊥平面ABCD,AD=3AB=3PA=3a。
,又PA⊥平面ABCD,AD=3AB=3PA=3a。