题目内容
如右放置在水平面上的组合体由直三棱柱 与正三棱锥
与正三棱锥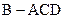 组成,其中,
组成,其中,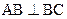 .它的正视图、俯视图、从左向右的侧视图的面积分别为
.它的正视图、俯视图、从左向右的侧视图的面积分别为 ,
, ,
, .
.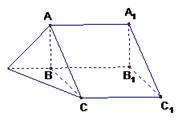
(Ⅰ)求直线 与平面
与平面 所成角的正弦;
所成角的正弦;
(Ⅱ)在线段 上是否存在点
上是否存在点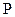 ,使
,使 平面
平面 .若存在,确定点
.若存在,确定点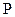 的位置;若不存在,说明理由.
的位置;若不存在,说明理由.
 与正三棱锥
与正三棱锥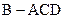 组成,其中,
组成,其中,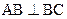 .它的正视图、俯视图、从左向右的侧视图的面积分别为
.它的正视图、俯视图、从左向右的侧视图的面积分别为 ,
, ,
, .
.
(Ⅰ)求直线
 与平面
与平面 所成角的正弦;
所成角的正弦;(Ⅱ)在线段
 上是否存在点
上是否存在点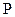 ,使
,使 平面
平面 .若存在,确定点
.若存在,确定点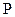 的位置;若不存在,说明理由.
的位置;若不存在,说明理由.(Ⅰ)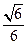 (Ⅱ)不存在
(Ⅱ)不存在
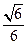 (Ⅱ)不存在
(Ⅱ)不存在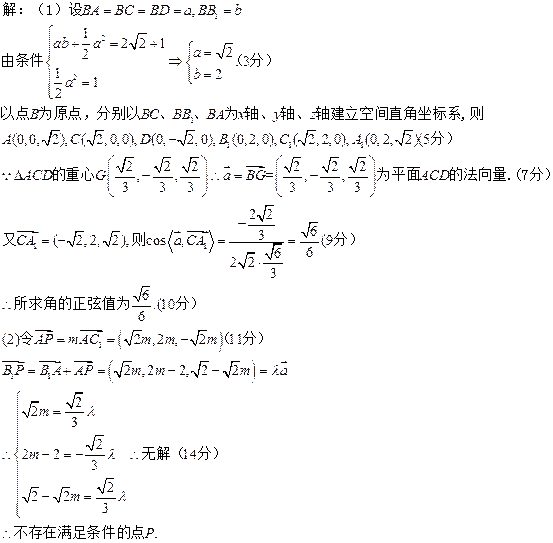

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
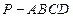 中,面
中,面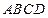 为矩形,
为矩形,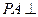 面
面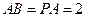
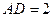 时,平面PBD⊥平面PAC;
时,平面PBD⊥平面PAC;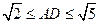 时,求二面角
时,求二面角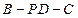 的取值范围。
的取值范围。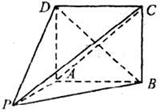
 中,
中,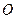 是
是 的中点,
的中点, ,
, .(Ⅰ)求证:
.(Ⅰ)求证: 平面
平面 ;(Ⅱ)求异面直线
;(Ⅱ)求异面直线 与
与 所成角的大小;
所成角的大小;
 的大小.
的大小.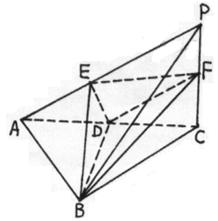
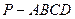 中,底面
中,底面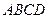 是矩形,已知
是矩形,已知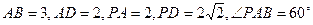 .
.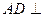 平面
平面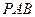 ;
;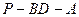 的大小.
的大小.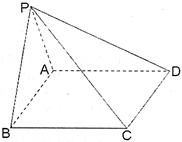
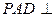 平面ABCD,ABCD为正方形,
平面ABCD,ABCD为正方形,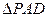 是直角三角形,且
是直角三角形,且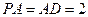 ,E、F、G分别是线段PA,PD,CD的中点.
,E、F、G分别是线段PA,PD,CD的中点.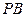 ∥面EFC;
∥面EFC;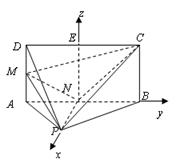
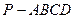 的底面为正方形,
的底面为正方形,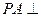 底面
底面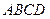 ,
, ,
,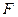 为
为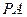 上的点.
上的点. ;
;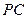 //平面
//平面 ,求二面角
,求二面角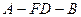 的余弦值.
的余弦值.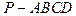 中,AD∥BC,∠ABC=90°,且
中,AD∥BC,∠ABC=90°,且 ,又PA⊥平面ABCD,AD=3AB=3PA=3a。
,又PA⊥平面ABCD,AD=3AB=3PA=3a。
 .
. .
. .
. .
.