题目内容
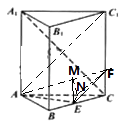
【题目】已知正三棱柱ABC﹣A1B1C1的各个棱长都相等,E为BC的中点,动点F在CC1上,且不与点C重合
(1)当CC1=4CF时,求证:EF⊥A1C
(2)设二面角C﹣AF﹣E的大小为α,求tanα的最小值.
【答案】
(1)证明:过E作EN⊥AC于N,连接EF,NF,AC1,
由直棱柱的性质可知,底面ABC⊥侧面A1C,
∴EN⊥侧面A1C,NF为EF在侧面A1C内的射影,
设正三棱柱ABC﹣A1B1C1的各个棱长为4,
∵CC1=4CF,∴在直角三角形CNF中,CN=1,
则由 ![]() =
= ![]() =
= ![]() ,得NF∥AC1,
,得NF∥AC1,
又AC1⊥A1C,故NF⊥A1C,
由三垂线定理可知EF⊥A1C
(2)解:连接AF,过N作NM⊥AF于M,连接ME
由(I)可知EN⊥侧面A1C,根据三垂线定理得EM⊥AF
∴∠EMN是二面角C﹣AF﹣E的平面角即∠EMN=α,
设∠FAC=θ,则0°<θ≤45°,
在直角三角形CNE中,NE= ![]() ,
,
在直角三角形AMN中,MN=3sinθ
故tanα= ![]() ,又0°<θ≤45°,∴0<sinθ≤
,又0°<θ≤45°,∴0<sinθ≤ ![]()
故当θ=45°时,tanα达到最小值,
∴tanα的最小值为anα= ![]() .
.
【解析】(1)过E作EN⊥AC于N,连接EF,NF,AC1 , 则EN⊥侧面A1C,NF为EF在侧面A1C内的射影,设正三棱柱ABC﹣A1B1C1的各个棱长为4,则CN=1,NF∥AC1 , 推导出C1⊥A1C,NF⊥A1C,由此能证明EF⊥A1C.(2)连接AF,过N作NM⊥AF于M,连接ME,则EN⊥侧面A1C,根据三垂线定理得EM⊥AF,∠EMN是二面角C﹣AF﹣E的平面角由此能示出tanα的最小值.
【考点精析】解答此题的关键在于理解空间中直线与直线之间的位置关系的相关知识,掌握相交直线:同一平面内,有且只有一个公共点;平行直线:同一平面内,没有公共点;异面直线: 不同在任何一个平面内,没有公共点.

 阅读快车系列答案
阅读快车系列答案【题目】某企业员工500人参加“学雷锋”志愿活动,按年龄分组:第1组[25,30),第2组[30,35),第3组[35,40),第4组[40,45),第5组[45,50],得到的频率分布直方图如图: 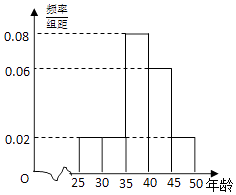
(1)如表是年龄的频数分布表,求a,b的值;
区间 | [25,30) | [30,35) | [35,40) | [40,45) | [45,50] |
人数 | 50 | 50 | a | 150 | b |
(2)根据频率分布直方图估计志愿者年龄的平均数和中位数;
(3)现在要从年龄较小的第1,2,3组中用分层抽样的方法抽取6人,则年龄在第1,2,3组的分别抽取多少人?
(4)在(3)的前提下,从这6人中随机抽取2人参加社区宣传交流活动,求至少有1人年龄在第3组的概率.