��Ŀ����
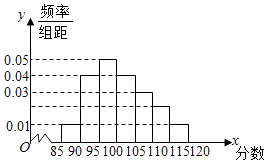
����Ŀ��ijУ�Ӳμӿ��Ե�ѧ���г��60��ѧ��������ɼ�����Ϊ�������ֳ�����[40��50����[50��60��[90��100]�������²���Ƶ�ʷֲ�ֱ��ͼ���۲�ͼ�ε���Ϣ���ش��������⣺ 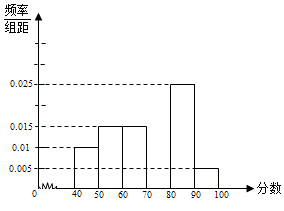
���� ��ɼ�����[70��80���ϵ�Ƶ�ʣ�����ȫ���Ƶ�ʷֲ�ֱ��ͼ��
���� ������ο��Եļ����ʣ�60�ּ�����Ϊ����ƽ���֣�
���� ��ѧ���ס��ҵijɼ���������[40��50�����ִӳɼ����ڸ������ѧ������ѡ���ˣ���ס�����������һ�˱�ѡ�ĸ��ʣ�
���𰸡��⣺������Ƶ�ʷֲ�ֱ��ͼ�ã�
�ɼ�����[70��80���ϵ�Ƶ���ǣ�1����0.01+0.015+0.015+0.025+0.005����10=0.3��
��ȫ���Ƶ�ʷֲ�ֱ��ͼ����ͼ��
���� ������ο��Եļ����ʣ�60�ּ�����Ϊ����
Ϊ1��0.01��10��0.015��10=75%
ƽ���֣�45��0.1+55��0.15+65��0.15+75��0.3+85��0.25+95��0.05=71��
������ѧ���ס��ҵijɼ���������[40��50����
����[40��50�����У�60��0.01��10=6��ѧ����
�ִӳɼ����ڸ������ѧ������ѡ���ˣ�
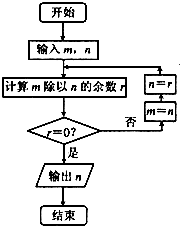
�����¼�����n= ![]() =15��
=15��
�ס�����������һ�˱�ѡ�Ķ����¼��Ǽס�������û��ѡ��
��ס�����������һ�˱�ѡ�ĸ���p=1�� ![]() =
= ![]() ��
��
��������������Ƶ�ʷֲ�ֱ��ͼ������ɼ�����[70��80���ϵ�Ƶ�ʣ��ɴ��ܲ�ȫ���Ƶ�ʷֲ�ֱ��ͼ����������Ƶ�ʷֲ�ֱ��ͼ�ܹ�����ο��Եļ����ʣ�60�ּ�����Ϊ����ƽ���֣�������ѧ���ס��ҵijɼ���������[40��50��������[40��50������6��ѧ�����ִӳɼ����ڸ������ѧ������ѡ���ˣ������¼�����n= ![]() =15���ס�����������һ�˱�ѡ�Ķ����¼��Ǽס�������û��ѡ���ɴ����ö����¼����ʼ��㹫ʽ������ס�����������һ�˱�ѡ�ĸ��ʣ�
=15���ס�����������һ�˱�ѡ�Ķ����¼��Ǽס�������û��ѡ���ɴ����ö����¼����ʼ��㹫ʽ������ס�����������һ�˱�ѡ�ĸ��ʣ�
�����㾫����������Ŀ����֪����������Ƶ�ʷֲ�ֱ��ͼ�����֪ʶ���Եõ�����Ĵ𰸣���Ҫ����Ƶ�ʷֲ�����Ƶ�ʷֲ�ֱ��ͼ���Ƕ���ͬ���ݵ����ֲ�ͬ���﷽ʽ.�ý��յı���ı����ݵ����з�ʽ������ʽ����չʾ���ݵķֲ����.ͨ����ͼ�ȿ��Դ���������ȡ��Ϣ���ֿ�������ͼ�δ�����Ϣ��

����Ŀ��ijУ�߶�������N��ѧ�������������ɼ�������120�֣��ֲ�ֱ��ͼ��ͼ����֪������100��110��ѧ������21�ˣ� ������������N�ͷ�����110��115�ֵ�����n��
���������ӷ�����110��115�ֵ�n��ѧ����Ů��ռ ![]() ������ѡ2�ˣ�������ǡ�ú���һ��Ů���ĸ��ʣ�
������ѡ2�ˣ�������ǡ�ú���һ��Ů���ĸ��ʣ�
����Ϊ�˷���ij��ѧ����ѧϰ״̬��������һ�ε�ѧϰ�ṩָ���Խ��飬����ǰ7�ο��Ե���ѧ�ɼ�x������150�֣��������ɼ�y���з����������Ǹ���7�ο��Եijɼ���
��ѧ | 88 | 83 | 117 | 92 | 108 | 100 | 112 |
���� | 94 | 91 | 108 | 96 | 104 | 101 | 106 |
��֪�����������ɼ�y����ѧ�ɼ�x��������صģ�����������ѧ�ɼ��ﵽ130�֣�����������������ɼ���Լ�Ƕ��٣�
��������һ�����ݣ�u1 �� v1������u2 �� v2��������un �� vn������ع���v=��+��u��б�ʺͽؾ����С���˹��Ʒֱ�Ϊ 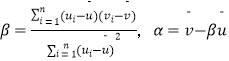 ��
��