题目内容
【题目】我国是世界上严重缺水的国家之一,城市缺水问题较为突出.某市政府为了鼓励居民节约用水,计划调整居民生活用水收费方案,拟确定一个合理的月用水量标准x(吨),一位居民的月用水量不超过x的部分按平价收费,超出x的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5)分成9组,制成了如图所示的频率分布直方图. (Ⅰ)求直方图中a的值;
(Ⅱ)若该市有110万居民,估计全市居民中月均用水量不低于3吨的人数,请说明理由;
(Ⅲ)若该市政府希望使80%的居民每月的用水量不超过标准x(吨),估计x的值(精确到0.01),并说明理由.
【答案】解:(Ⅰ)由概率统计相关知识,各组频率和为1, 即0.5×(0.08+0.16+0.3+a+0.52+0.3+0.12+0.08+0.04)=1,
解得a=0.4;
(Ⅱ)由图知,不低于3吨的人数所占比例为
0.5×(0.12+0.08+0.04)=0.12,
∴全市月均用水量不低于3吨的人数为
110×0.12=13.2(万);
(Ⅲ)由图可知,月均用水量小于2.5吨的居民人数所占比例为
0.5×(0.08+0.16+0.3+0.4+0.52)=0.73,
即73%的居民月均用水量小于2.5吨;
同理,88%的居民月均用水量小于3吨,故2.5<x<3;
假设月均用水量平均分布,则![]() (吨)
(吨)
【解析】(Ⅰ)由概率统计相关知识,各组频率和为1,列出方程求出a的值;(Ⅱ)由图计算不低于3吨的频率和频数即可;(Ⅲ)由图计算月均用水量小于2.5吨的频率和月均用水量小于3吨的频率, 假设月均用水量平均分布,由此求出x的值.
【考点精析】本题主要考查了频率分布直方图的相关知识点,需要掌握频率分布表和频率分布直方图,是对相同数据的两种不同表达方式.用紧凑的表格改变数据的排列方式和构成形式,可展示数据的分布情况.通过作图既可以从数据中提取信息,又可以利用图形传递信息才能正确解答此题.

 暑假作业海燕出版社系列答案
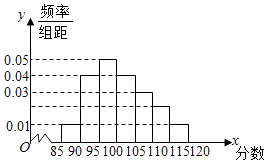
暑假作业海燕出版社系列答案【题目】某校高二奥赛班N名学生的物理测评成绩(满分120分)分布直方图如图,已知分数在100~110的学生数有21人. (Ⅰ)求总人数N和分数在110~115分的人数n;
(Ⅱ)现准备从分数在110~115分的n名学生(女生占 ![]() )中任选2人,求其中恰好含有一名女生的概率;
)中任选2人,求其中恰好含有一名女生的概率;
(Ⅲ)为了分析某个学生的学习状态,对其下一阶段的学习提供指导性建议,对他前7次考试的数学成绩x(满分150分),物理成绩y进行分析,下面是该生7次考试的成绩.
数学 | 88 | 83 | 117 | 92 | 108 | 100 | 112 |
物理 | 94 | 91 | 108 | 96 | 104 | 101 | 106 |
已知该生的物理成绩y与数学成绩x是线性相关的,若该生的数学成绩达到130分,请你估计他的物理成绩大约是多少?
附:对于一组数据(u1 , v1),(u2 , v2),,(un , vn),其回归线v=α+βu的斜率和截距的最小二乘估计分别为 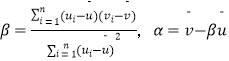 .
.