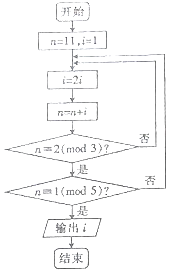
题目内容
【题目】某企业员工500人参加“学雷锋”志愿活动,按年龄分组:第1组[25,30),第2组[30,35),第3组[35,40),第4组[40,45),第5组[45,50],得到的频率分布直方图如图: 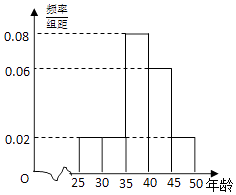
(1)如表是年龄的频数分布表,求a,b的值;
区间 | [25,30) | [30,35) | [35,40) | [40,45) | [45,50] |
人数 | 50 | 50 | a | 150 | b |
(2)根据频率分布直方图估计志愿者年龄的平均数和中位数;
(3)现在要从年龄较小的第1,2,3组中用分层抽样的方法抽取6人,则年龄在第1,2,3组的分别抽取多少人?
(4)在(3)的前提下,从这6人中随机抽取2人参加社区宣传交流活动,求至少有1人年龄在第3组的概率.
【答案】
(1)解:由频率分布直方图知:
a=0.08×5×500=200,
b=0.02×5×500=50.
(2)解:由频率分布直方图估计志愿者年龄的平均数为:
27.5×0.02×5+32.5×0.02×5+37.5×0.08×5+42.5×0.06×5+47.5×0.02×5=38.5,
∵[25,35)上的频率为(0.02+0.02)×5=0.2,[35,40)上的频率为0.08×5=0.4,
∴中位数为:35+ ![]() =38.75.
=38.75.
和中位数
(3)解:因为第1,2,3组共有50+50+200=300人,
利用分层抽样在300名学生中抽取6名学生,每组抽取的人数分别为:
第1组的人数为6× ![]() =1,
=1,
第2组的人数为6× ![]() =1,
=1,
第3组的人数为6× ![]() =4,
=4,
所以第1,2,3组分别抽取1人,1人,4人
(4)解:设第1组的1位同学为A,第2组的1位同学为B,
第3组的4位同学为C1,C2,C3,C4,
则从六位同学中抽两位同学有:
(A,B),(A,C1),(A,C2),(A,C3),(A,C4),(B,C1),(B,C2),(B,C3),
(B,C4),(C1,C2),(C1,C3),(C1,C4),(C2,C3),(C2,C4),(C3,C4),共15种可能.
其中恰有1人年龄在第3组有8种可能,
所以恰有1人年龄在第3组的概率为P= ![]()
【解析】(1)根据频率分布直方图求频率,由此能求出a,b的值.(2)根据频率分布直方图能估计志愿者年龄的平均数和中位数.(3)利用样本容量比总容量的比例计算.(4)利用第2问的结论,列出所有可能情况,在其中挑出符合题意的情况,求比值.
【考点精析】解答此题的关键在于理解频率分布直方图的相关知识,掌握频率分布表和频率分布直方图,是对相同数据的两种不同表达方式.用紧凑的表格改变数据的排列方式和构成形式,可展示数据的分布情况.通过作图既可以从数据中提取信息,又可以利用图形传递信息,以及对平均数、中位数、众数的理解,了解⑴平均数、众数和中位数都是描述一组数据集中趋势的量;⑵平均数、众数和中位数都有单位;⑶平均数反映一组数据的平均水平,与这组数据中的每个数都有关系,所以最为重要,应用最广;⑷中位数不受个别偏大或偏小数据的影响;⑸众数与各组数据出现的频数有关,不受个别数据的影响,有时是我们最为关心的数据.