题目内容
【题目】某班50位学生周考数学成绩的频率分布直方图如图所示,其中成绩分组区间是:![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() .
.

(1)求图中![]() 的矩形高的值,并估计这50人周考数学的平均成绩;
的矩形高的值,并估计这50人周考数学的平均成绩;
(2)根据直方图求出这50人成绩的众数和中位数(精确到0.1);
(3)从成绩不低于80分的学生中随机选取2人,该2人中成绩不低于90分的人数记为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
【答案】(1)高的值为![]() ;平均成绩为74;(2)众数为75.0,中位数
;平均成绩为74;(2)众数为75.0,中位数![]() ;(3)分布列见解析,
;(3)分布列见解析,![]()
【解析】
(1)由频率和为1列出方程求解![]() 的矩形高,频率分布直方图中每个小长方形的面积乘以小长方形底边中点的横坐标之和即为平均数;(2)最高矩形的中间值为众数,根据中位数左右两边的矩形面积相等列出等式求解中位数;(3)分别求出成绩不低于80分、成绩不低于90分的人数,则
的矩形高,频率分布直方图中每个小长方形的面积乘以小长方形底边中点的横坐标之和即为平均数;(2)最高矩形的中间值为众数,根据中位数左右两边的矩形面积相等列出等式求解中位数;(3)分别求出成绩不低于80分、成绩不低于90分的人数,则![]() 可取0,1,2,利用古典概型概率计算公式分别求出
可取0,1,2,利用古典概型概率计算公式分别求出![]() 的概率,列出分布列,求出数学期望.
的概率,列出分布列,求出数学期望.
(1)设图中![]() 的矩形高为
的矩形高为![]() ,则
,则![]() ,
,
解得![]() ,
,
平均成绩为![]() .
.
(2)由直方图可知,其数据的众数为最高矩形的中间值,所以众数为75.0;
设中位数为![]() ,则中位数左右两边的矩形面积相等,即左右频率各为0.5,
,则中位数左右两边的矩形面积相等,即左右频率各为0.5,
故![]() ,解得
,解得![]() .
.
(3)成绩不低于80分的学生有![]() 人,其中成绩不低于90分的人数为
人,其中成绩不低于90分的人数为![]() 人,随机变量
人,随机变量![]() 可取0,1,2,
可取0,1,2,
![]() ,
,![]() ,
,![]() ,
,
分布列为

![]() .
.

练习册系列答案
相关题目
【题目】某地区2007年至2011年农村居民家庭纯收入y(单位:千元)的数据如下表:
年份 | 2007 | 2008 | 2009 | 2010 | 2011 |
年份代号t | 1 | 2 | 3 | 4 | 5 |
人均纯收入y | 3.1 | 3.6 | 3.9 | 4.4 | 5 |
(1)求y关于t的线性回归方程;
(2)利用(1)中的回归方程,分析2007年至2011年该地区农村居民家庭人均纯收入的变化情况,并预测该地区2015年农村居民家庭人均纯收入.
附:回归直线的斜率和截距的最小二乘法估计公式分别为: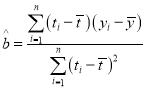 ,
,![]()