题目内容
【题目】已知等差数列{an}的前n项和为Sn , 且S6=5S2+18,a3n=3an , 数列{bn}满足b1b2…bn=4Sn . (Ⅰ)求数列{an},{bn}的通项公式;
(Ⅱ)令cn=log2bn , 且数列 ![]() 的前n项和为Tn , 求T2016 .
的前n项和为Tn , 求T2016 .
【答案】解:(Ⅰ)设数列{an}的公差为d, 则 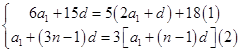
由(1)得2a1﹣5d+9=0,
由(2)得a1=d,联立得a1=d=3,
所以an=3n.
易知b1=64,
当n≥2时 ![]() ,又
,又 ![]() ,
,
两式相除得 ![]() , b1=64满足上式,所以
, b1=64满足上式,所以 ![]() .
.
(Ⅱ) ![]() ,
, ![]() ,
,![]() ,
,
因此 ![]() .
.
【解析】(I)利用等差数列的通项公式可得an , 利用递推关系可得bn . (II)cn=log2bn=6n, ![]() =
= ![]() =
= ![]() ,利用“裂项求和”方法即可得出.
,利用“裂项求和”方法即可得出.
【考点精析】认真审题,首先需要了解数列的前n项和(数列{an}的前n项和sn与通项an的关系 ),还要掌握数列的通项公式(如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式)的相关知识才是答题的关键.
),还要掌握数列的通项公式(如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式)的相关知识才是答题的关键.

练习册系列答案
相关题目