题目内容
【题目】已知函数f(x)=|x+2|﹣2|x﹣1|. (Ⅰ)求不等式f(x)≥﹣2的解集M;
(Ⅱ)对任意x∈[a,+∞),都有f(x)≤x﹣a成立,求实数a的取值范围.
【答案】解:(Ⅰ)f(x)=|x+2|﹣2|x﹣1|≥﹣2, 当x≤﹣2时,x﹣4≥﹣2,即x≥2,所以x∈;
当﹣2<x<1时,3x≥﹣2,即x≥﹣ ![]() ,所以﹣
,所以﹣ ![]() ≤x<1;
≤x<1;
当x≥1时,﹣x+4≥﹣2,即x≤6,所以1≤x≤6;
综上,不等式f(x)≥﹣2的解集为M={x|﹣ ![]() ≤x≤6};
≤x≤6};
(Ⅱ)f(x)= 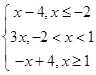 ,
,
令y=x﹣a,当直线经过点(1,3)时,﹣a=2,
所以当﹣a≥2,即a≤﹣2时成立;
当﹣a<2即a>﹣2时,令﹣x+4=x﹣a,得x=2+ ![]() ,
,
所以a≥2+ ![]() ,即a≥4,
,即a≥4,
综上,a≤﹣2或a≥4.
解法二:(Ⅰ)同解法一,
(Ⅱ)设g(x)=f(x)﹣x= 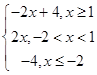 ,
,
因为对任意x∈[a,+∞),都有f(x)≤x﹣a成立,
所以﹣a≥g(x)max ,
①当a>1时,g(x)max=g(a)=﹣2a+4,
所以﹣a≥﹣2a+4,所以a≥4,符合a>1.
②当a≤1时,g(x)max=g(1)=2,
所以﹣a≥2,所以a≤﹣2,符合a≤1,
综上,实数a的取值范围是(﹣∞,﹣2]∪[4,+∞).
【解析】(Ⅰ)通过讨论x的范围,求出各个区间上的不等式的解集,取并集即可;(Ⅱ)法一:求出f(x)的分段函数的形式,令y=x﹣a,通过讨论求出a的范围即可;法二:设g(x)=f(x)﹣x,问题转化为﹣a≥g(x)max , 求出g(x)的最大值,得到a的范围即可.
【考点精析】掌握绝对值不等式的解法是解答本题的根本,需要知道含绝对值不等式的解法:定义法、平方法、同解变形法,其同解定理有;规律:关键是去掉绝对值的符号.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
