题目内容

12．已知数列{an}是等差数列，a1=16，d=-3，求Sn的最大值．

分析 求出等差数列的前n项和，结合一元二次函数的性质进行求解即可．

解答 解：∵等差数列{an}的首项a1=16，公差d=-3，
∴前n项和Sn=16n+$\frac{n（n-1）}{2}$×（-3）=-$\frac{3}{2}$n2+$\frac{35}{2}$n=-$\frac{3}{2}$（n-$\frac{35}{6}$）2+$\frac{1225}{24}$，
∴当n=6时，Sn取得最大值，最大值为S6=51．

点评 本题主要考查等差数列的前n项和公式的应用，结合一元二次函数的性质是解决本题的关键．

练习册系列答案
相关题目
10．如果对数logx+7（x2+6x+5）有意义，求x的取值范围．
3．已知M0是（x0，y0）是x2+y2=a2（a＞0）内一点，则判断l：x0x+y0y=a2与圆的位置关系．
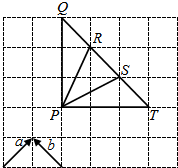20．如图所示，下列结论正确的是（　　）
①$\overrightarrow{PQ}$=$\frac{3}{2}$$\overrightarrow{a}$+$\frac{3}{2}$$\overrightarrow{b}$；②$\overrightarrow{PT}$=-$\frac{3}{2}$$\overrightarrow{a}$-$\frac{3}{2}$$\overrightarrow{b}$；③$\overrightarrow{PS}$=$\frac{3}{2}$$\overrightarrow{a}$-$\frac{1}{2}$$\overrightarrow{b}$；④$\overrightarrow{PR}$=$\frac{3}{2}$$\overrightarrow{a}$+$\overrightarrow{b}$．
A．①②B．③④C．①③D．②④
7．等差数列{an}的前n项和为Sn，已知a1=13，S3=S11，当Sn最大时，n的值是7．
17．求函数的值域，单调区间．
y=log${\;}_{\frac{1}{2}}$（x-1）-log${\;}_{\frac{1}{2}}$（x+3）
4．求函数y=log0.5（-x2+8）的值域及单调区间．
1．若f（x）的定义域为{x|x＞0，x∈R}，且f（x+y）=f（x）+f（y），若f（3）=1，则f（9）=3．
2．判断下列函数的奇偶性．
（1）f（x）=$\sqrt{1-{x}^{2}}$+$\sqrt{{x}^{2}-1}$；
（2）f（x）=$\frac{\sqrt{4-{x}^{2}}}{|x+3|-3}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网