题目内容
(满分14分)已知函数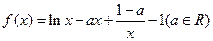
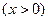
(1)当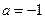 时,求曲线
时,求曲线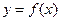 在点
在点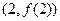 处的切线方程;
处的切线方程;
(2)当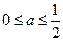 时,讨论
时,讨论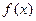 的单调性
的单调性
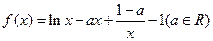
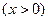
(1)当
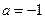 时,求曲线
时,求曲线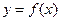 在点
在点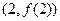 处的切线方程;
处的切线方程;(2)当
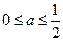 时,讨论
时,讨论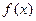 的单调性
的单调性(1)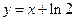
(2)当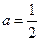 时,
时,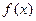 在
在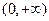 上单调递减;
上单调递减;
当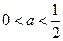 时,
时,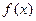 在
在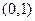 和
和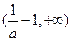 上单调递减,在
上单调递减,在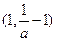 上单调递增
上单调递增
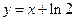
(2)当
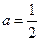 时,
时,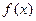 在
在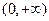 上单调递减;
上单调递减;当
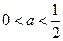 时,
时,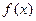 在
在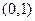 和
和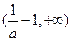 上单调递减,在
上单调递减,在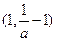 上单调递增
上单调递增解:(1)当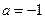 时,
时, ,则
,则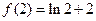 ,又
,又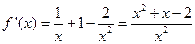 ,则曲线
,则曲线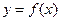 在点
在点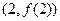 处的切线斜率为
处的切线斜率为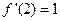 ,因此,切线方程为
,因此,切线方程为 ,即
,即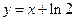
(2)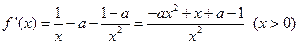 ,设
,设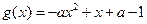 ,
,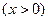 ,则
,则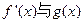 符号相同。
符号相同。
①若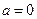 ,
,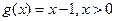 ,
,
当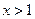 时,
时,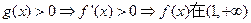 上单调递增;
上单调递增;
当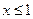 时,
时,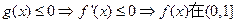 上单调递减。
上单调递减。
②若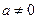 ,则
,则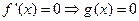 ,即
,即 ,解得
,解得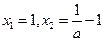 。
。
当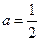 时,
时,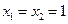 ,
,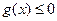 恒成立,即
恒成立,即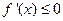 恒成立,因此
恒成立,因此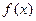 在
在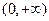 上单调递减;
上单调递减;
当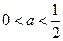 时,
时,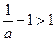 。可列表如下:
。可列表如下:
综上所述:当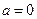 时,
时,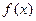 在
在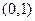 上单调递减,在
上单调递减,在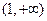 单调递增;
单调递增;
当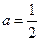 时,
时,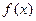 在
在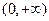 上单调递减;
上单调递减;
当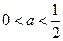 时,
时,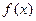 在
在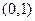 和
和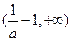 上单调递减,在
上单调递减,在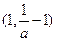 上单调递增。
上单调递增。
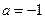 时,
时, ,则
,则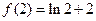 ,又
,又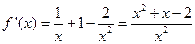 ,则曲线
,则曲线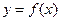 在点
在点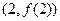 处的切线斜率为
处的切线斜率为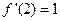 ,因此,切线方程为
,因此,切线方程为 ,即
,即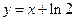
(2)
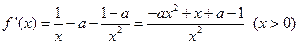 ,设
,设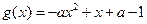 ,
,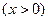 ,则
,则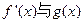 符号相同。
符号相同。①若
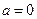 ,
,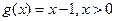 ,
,当
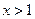 时,
时,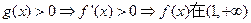 上单调递增;
上单调递增;当
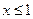 时,
时,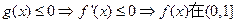 上单调递减。
上单调递减。②若
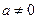 ,则
,则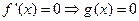 ,即
,即 ,解得
,解得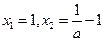 。
。当
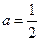 时,
时,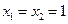 ,
,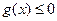 恒成立,即
恒成立,即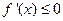 恒成立,因此
恒成立,因此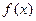 在
在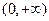 上单调递减;
上单调递减;当
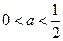 时,
时,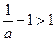 。可列表如下:
。可列表如下: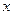 | 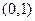 | 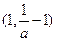 | 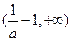 |
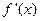 (与 (与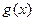 符号一致) 符号一致) | 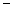 | 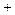 |  |
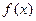 |  |  | 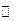 |
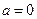 时,
时,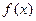 在
在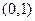 上单调递减,在
上单调递减,在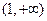 单调递增;
单调递增;当
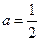 时,
时,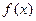 在
在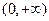 上单调递减;
上单调递减;当
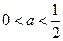 时,
时,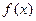 在
在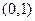 和
和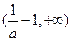 上单调递减,在
上单调递减,在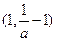 上单调递增。
上单调递增。
练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
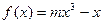 以
以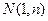 为切点的切线的倾斜角为
为切点的切线的倾斜角为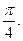
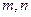 的值;
的值;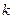 ,使得不等式
,使得不等式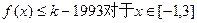 恒成立?如果存在,请求出最小的正整数
恒成立?如果存在,请求出最小的正整数 在
在 点
点 处的切线方程。
处的切线方程。 在点
在点 处切线为
处切线为 (如图),设
(如图),设 ,则( )
,则( ) 的极大值点
的极大值点 的极值点
的极值点 的极值点
的极值点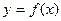 的图象在点
的图象在点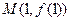 处的切线方程是
处的切线方程是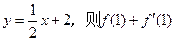 = 。
= 。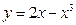 在
在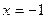 处的切线方程为 。
处的切线方程为 。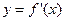 是函数
是函数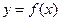 的导函数,且函数
的导函数,且函数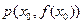 处的切线为
处的切线为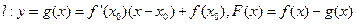 ,如果函数
,如果函数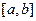 上的图像如图所示,且
上的图像如图所示,且 ,那么( )
,那么( ) 是
是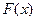 的极大值点
的极大值点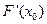 =
=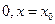 是
是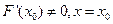 不是
不是
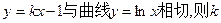 = 。
= 。